Question

Draw a right triangle in which the sides (other than hypotenuse) are of lengths \[5\;cm\] and \[4{\text{ }}cm\] .Then construct another triangle whose sides are $ \dfrac{5}{3} $ times the corresponding sides of the given triangle.

Answer 1

Hint: Draw the given triangle and then using scale factor draw the next triangle

First, we draw a rough sketch and then we are going to construct the triangle whose two sides are given in the question. Then we are given another triangle, so by scale factor properties we will draw the next required triangle by extending the ray, then dividing the ray at the unit length and then drawing parallel lines at the scale values and then completing the triangle.

Complete step-by-step answer:
Let’s draw a rough diagram first.

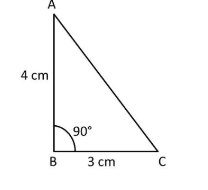
For constructing this, the steps are
I.Draw base \[BC\] of side \[3{\text{ }}\;cm\]
II.Draw \[B = {90^o}\]
III.Taking B as centre, \[4\;cm\] as radius, we draw an arc
IV.Let the point where arc intersects the ray be point A
Join \[AC\]

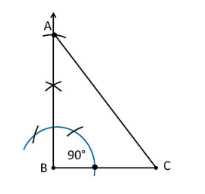
 $ \vartriangle ABC $ is the required triangle.

Now, we have to make a triangle which is $ \dfrac{5}{3} $ times its size.

STEPS OF CONSTRUCTION
A.Draw any ray $ BX $ making an acute angle with BC on the side opposite side to the vertex A.

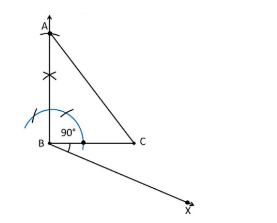
B.Mark 5 (the greater of 5 and 3 in $ \dfrac{5}{3} $ ) points $ {B_1},{B_2},{B_3},{B_4},{B_5} $ on $ BX $ such that $ B{B_1} = {B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4} = {B_4}{B_5} $

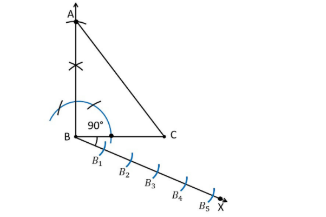
C.Join \[BC\] (3rd point as 3 is smaller in $ \dfrac{5}{3} $ ) and draw a line through B parallel to \[BC\] , to intersect BC extended at \[A'\] .

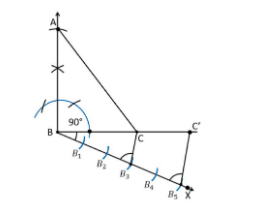
D.Draw a line through \[C'\] parallel to the line \[AC\] to intersect \[AB\] extended at \[A'\] .

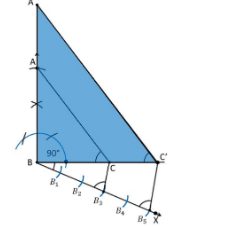
The above is required and a triangle whose side is whose sides are $ \dfrac{5}{3} $ times the corresponding sides of the given triangle.

Note: When we draw the extended ray, we have to make sure the ray is marked according to the highest of the difference factors and the divisions are in equal measurements to each other.