Question

Draw a ray diagram to show the image formation by the combination of two thin convex lenses to contact. Obtain the expression for the power of this combination in terms of the focal length of the lenses.

Answer 1

Hint: For this question we have to use the lens formula and power of lens formula. As two lenses are used, the image of the first lens will act as an object for the second lens. The principle and rules of ray optics are necessary for solving this problem.
Formula used:
Mirror formula- \[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]
Power of lens - \[P=\dfrac{1}{f}\]

Complete step by step solution:
Let us consider two lenses be \[{{L}_{1}}\], \[{{L}_{2}}\] having optical centres \[{{C}_{1}}\]and \[{{C}_{2}}\] respectively. Let \[{{f}_{1}}\] and \[{{f}_{2}}\] be focal length of lens \[{{L}_{1}}\] and \[{{L}_{2}}\]. Below is the ray diagram representing the path the light ray has travelled to form an image. The object is placed at O and passes through lens \[{{L}_{1}}\]and \[{{L}_{2}}\]forming an image at P then this image will act as an object for lens \[{{L}_{2}}\] and final image is formed at I.

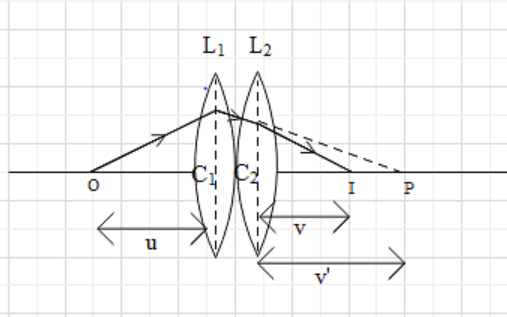
The distance between object O and \[{{C}_{1}}\]is represented as \[u\], distance between \[{{C}_{2}}\] and I is \[v\] and distance between \[{{C}_{2}}\] to P is \[{{v}^{'}}\].
Applying lens formula for convex lens \[{{L}_{1}}\]
 \[\dfrac{1}{{{f}_{1}}}=\dfrac{1}{{{v}^{'}}}-\dfrac{1}{u}\]…….. (1)
Similarly for lens \[{{L}_{2}}\],
\[\dfrac{1}{{{f}_{2}}}=\dfrac{1}{v}-\dfrac{1}{{{v}^{'}}}\]……... (2)
For the lens \[{{L}_{2}}\], P will act as virtual image object
Adding equation (1) and (2)
\[\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}=\dfrac{1}{v}-\dfrac{1}{u}\]
\[\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}\]
Where, $F$ be the focal length of the combined lens.
Power of lens is given by
\[P=\dfrac{1}{F}\]
Therefore power of combined lens
\[P=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}\]
Hence the answer has been calculated.

Note: The sign used in the formula should be taken care of properly. As two lenses are there, one should always solve for lens 1, the result of which will be used for lens 2. A ray diagram should always be drawn with a sharp pencil and the direction of the ray should be marked properly.