Question

Draw a ray diagram to show how a converging lens is able to form the image of the sun.

Answer 1

Hint : Since, the sun is very far, it can be assumed that the rays of light coming from it are parallel. Parallel rays focus at the focal point after striking a lens.

Formula used: In this solution we will be using the following formula;
 $ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} $ where $ f $ is the focal length of the convex lens, $ u $ is the distance of the object from the lens, and $ v $ is the distance of the image from the lens.

Complete step by step answer

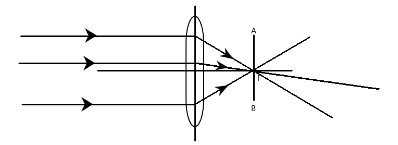
We are asked to show how a converging lens (also known as convex lens) can be used to form the image of the sun using a ray diagram. To do this, we must note that the sun is very far away, hence, objects can be said to be at infinity. In this situation, all rays of light coming from the object striking the lens can be said to be parallel to each other.
Now, as a rule of drawing ray diagrams, all rays of light parallel to the optical (or principal) axis of the lens, must be drawn to converge at the focal point of the lens, hence the image of the sun will be formed on a screen AB at the focal point as shown in the diagram. It used to largely be diminished.

Note
For clarity, mathematically, it can be proven that an object at infinity would produce its image at the focal point.
From the thin lens equation
 $ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} $ where $ f $ is the focal length of the convex lens, $ u $ is the distance of the object from the lens, and $ v $ is the distance of the image from the lens.
Hence, if $ u = \infty $
 $ \dfrac{1}{f} = \dfrac{1}{\infty } + \dfrac{1}{v} $
 $ \Rightarrow \dfrac{1}{f} = \dfrac{1}{v} $
Then by inverting
 $ v = f $ .