Question

Draw a line segment PQ = 8.5cm. Draw its perpendicular bisector. Take any point x on the Bisector.

Answer 1

Hint: First draw a line and mark point P. Then with a radius of 8.5cm intersect an arc with the line. The point of intersection is point Q. Now from point P with any radius say a cm such that $a> \dfrac{8.5}{2}= 4.25$, draw an arc above the line and below the line. Now with this same radius draw another arc from Q that intersects the arcs drawn in the previous step. Now through the point of intersection of both arcs draw a line. This line is the perpendicular bisector of line PQ. Let this line intersect PQ at O. Now from O with any radius r draw an arc which cuts the bisector and name the point x.

Complete step-by-step solution:
Now we will construct the line PQ and its bisector
STEP 1.
To draw the line PQ first draw any line and mark point P on it

STEP 2.
Now with center P and radius 8.5cm draw an arc, which intersects the above line. Name the point of intersection as Q.

STEP 3.
Now again with center P and take radius anything greater than half the distance PQ,
Let us say we have taken radius a cm. then $a> \dfrac{8.5}{2}= 4.25 cm$
Make an arc above the line as well as below the line from point P with a radius a cm.

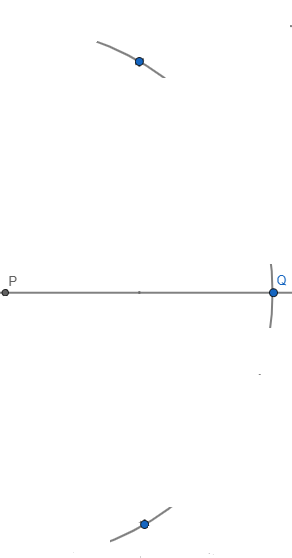
STEP 4.
Now with the same radius, a cm draw an arc from point Q above the line and below the line

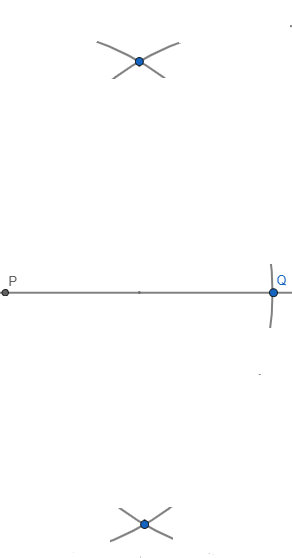
STEP 5.
Now join the intersection point of the two arcs.
The line that we get is the perpendicular bisector of PQ. Let is cut PQ at point O.

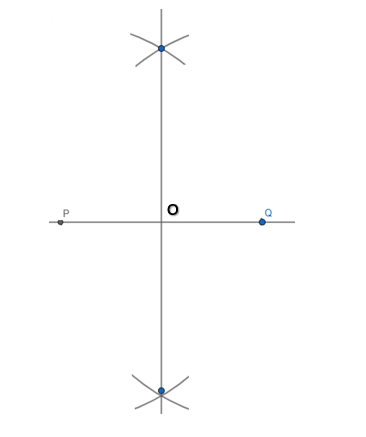
STEP 6.
Now from point O with any radius say r cm draw an arc which intersects the bisector. Name the point of intersection as O.

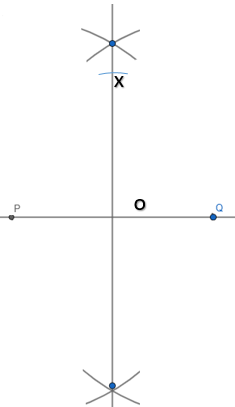
Hence now just label the line PQ with its distance which is 8.5cm.

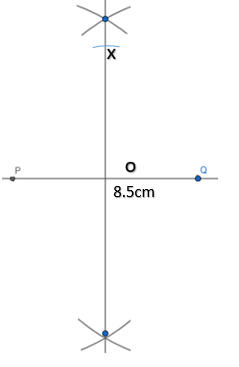
Note: Note that while drawing an arc in step 3, try to make the arc to somewhere near the center of the line to obtain a perfect diagram. Also, follow the exact procedure for precision do not just find a midpoint of line PQ and draw a perpendicular line through that.