Question

Draw a diagram to show how NAND gates can be combined to obtain an OR gate.

Answer 1

Hint: NAND gate and NOR gate are called universal gates since all simple gates like NOT, AND, and OR gates can be constructed using them. In the NAND gate, the two inputs are multiplied and the inverse is taken of the answer.
If A and B are two inputs to a NAND gate, the output is: $\overline {A.B} $
The formula used for converting NAND gate to OR gate is:
\[\overline {\overline A .\overline B } = A + B\]

Complete step by step solution:
If A and B are two inputs to a NAND gate, the output is: $\overline {A.B} $
To construct an OR gate from NAND gates, we need 3 NAND gates. Let us arrange them as shown in the circuit diagram:

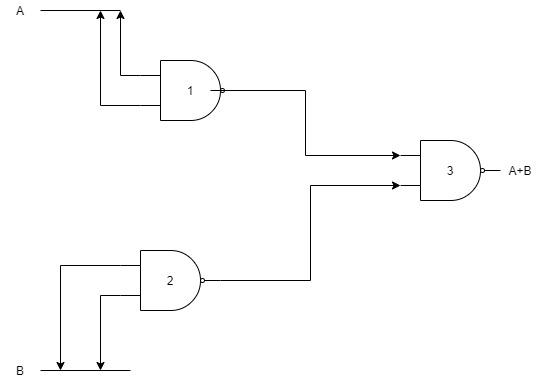
We will analyse the circuit by considering each of the NAND gates.

Step 1: NAND Gate -1
Input for the NAND gate = A and A
NAND operation = \[\overline {A.A} \]
Output = $\overline A $

Step 2: NAND Gate -1
Input for the NAND gate = B and B
NAND operation = \[\overline {B.B} \]
Output = $\overline B $

Step 1: NAND Gate -1
Input for the NAND gate = $\overline A $and $\overline B $
NAND operation =
 \[\overline {\overline A .\overline B } = \overline{\overline A} + \overline{\overline B} \]
Since double negative is positive,
\[\overline {\overline A .\overline B } = \overline{\overline A} + \overline{\overline B} = A + B\]
Output = $A + B$
The final output is equivalent to the OR gate:
$A||B = A + B$

$\therefore$Three NAND gates can be used to create an OR gate.

Note:
Sometimes, it becomes difficult to remember the conversion of Universal gates. You can easily remember the whole thing by understanding this mnemonic.
NAND Gate:
To convert to AND gate, first negate together because AND means together and negate the result.

To convert to OR gate, first negate them individually because OR means individually and negate the result.