Question

Draw a \[\Delta ABC\] whose sides are 4 cm, 6 cm and 3.5 cm respectively. Through A, draw a line parallel to BC.

Answer 1

Hint: For drawing a triangle with 3 given sides, we choose a side as a base. Then, we open our protractor to the given length of the side of the triangle, keep it out on any one end of the base and cut an arc. Then, we take the protractor to the other side of the base, open it again for the last remaining side and again cut an arc and intersect it with the first arc, and finally, we are going to have our triangle.

Complete step by step solution:
We need to construct a triangle follow the below steps
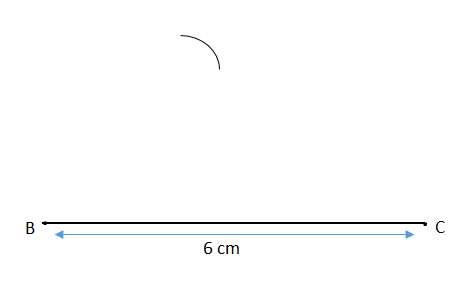
\[ \bullet \] Let consider that the base of a triangle is 6 cm and we name this side as BC.
Using a scale draw the base of length 6 cm.

\[ \bullet \] With B as a centre and 3.5 cm as radius draw an arc (using compass and scale)
That is

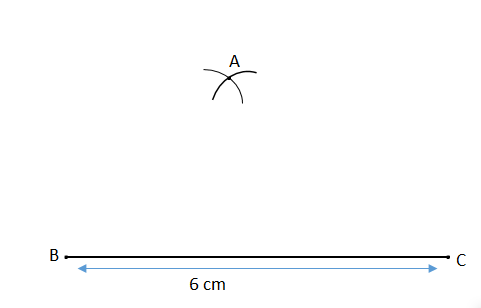
\[ \bullet \] Similarly with C as a centre and 4 cm as a radius draw an arc. We will get a point A. That is A is the point where two arcs intersect.

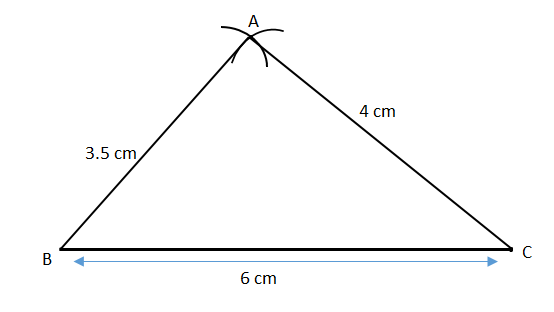
\[ \bullet \]Now we join B and A by straight line and A and C by straight line.

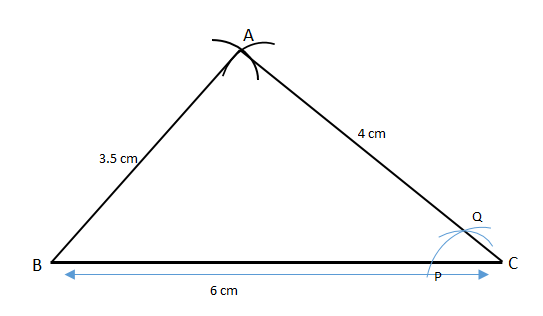
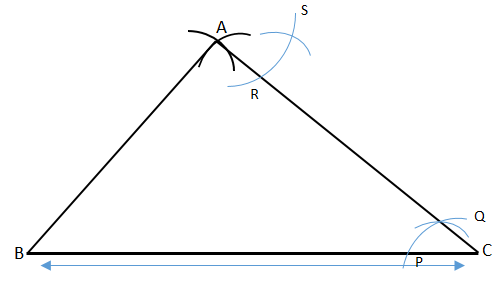
\[ \bullet \] Take a small radius, open the protractor at vertex C and construct an arc which cut AC and BC at P and Q respectively, and keep the protractor intact.

\[ \bullet \] Measure the arc PA using compass and cut the same arc length RS.
\[ \bullet \] Then, keeping the protractor opened with the same small radius, place it on A and draw an arc which cuts AC at R and cuts it till S.

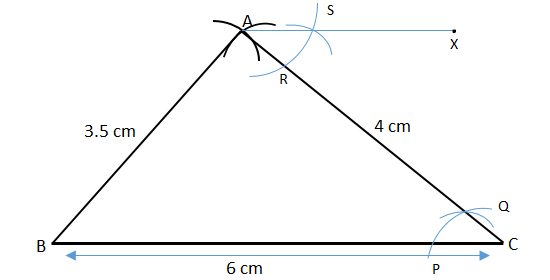
\[ \bullet \] Join AS and extend it till X.

Note: Follow the same procedure for these kinds of problems. We can choose any length for the base. We have chosen 6 cm as a base but we can also choose the remaining two lengths as a base. The way can be different but they are all going to lead to the same destination, or we could say they all are going to take us to the same result. The common out of the three ways is that we first choose a base, then we keep out our protractor at one end of the line (the base), open the given length and cut an arc. Then we repeat the same procedure from the other end of the base, and we are going to have our required resultant triangle. The final triangle is going to be the same, just the difference of orientation is going to be there.