Question

What is the domain and range of $y = \dfrac{1}{{x - 3}}$ ?

Answer 1

Hint:The domain of a graph refers to the set of potential input values. The domain of a function includes all of the input values of x displayed on the x-axis. The range of the function is the set of all the values that the function can assume. Range is the set of possible values of y for every value of x in the domain. For finding the domain of a rational function, we must ensure that the denominator is not equal to zero. Also, for finding the range of a function, we find x in the terms of y and find out the permissible values of y for x belonging to the domain.

Complete step by step answer:
So, we have, $y = \dfrac{1}{{x - 3}}$. We know that the denominator cannot be equal to zero.So, we set the denominator of the function not equal to zero and find the permissible values of $x$. This is because we cannot divide by zero, which means the denominator can't be zero.So, we get, $\left( {x - 3} \right) \ne 0$
\[ \Rightarrow x \ne 3\]

Thus, $x$ assumes all the real values of x except the number $3$. So, the domain of the function is $\left( { - \inf , - 3} \right) \cup \left( {3,\inf } \right)$. So, as we can see, $x$ does not equals three as the domain excludes the number. So, there is a discontinuity in the graph for $x = 3$. Now, for the range of the function, we find $x$ in terms of $y$.

So, we have, $y = \dfrac{1}{{x - 3}}$
$ \Rightarrow x - 3 = \dfrac{1}{y}$
Isolating x in left side of the equation, we get,
$ \Rightarrow x = \dfrac{1}{y} + 3$
Taking LCM of the denominators, we get,
$ \Rightarrow x = \dfrac{{1 + 3y}}{y}$
Now, we know that the denominator of a rational function cannot be zero.
Hence, we get, $y \ne 0$.

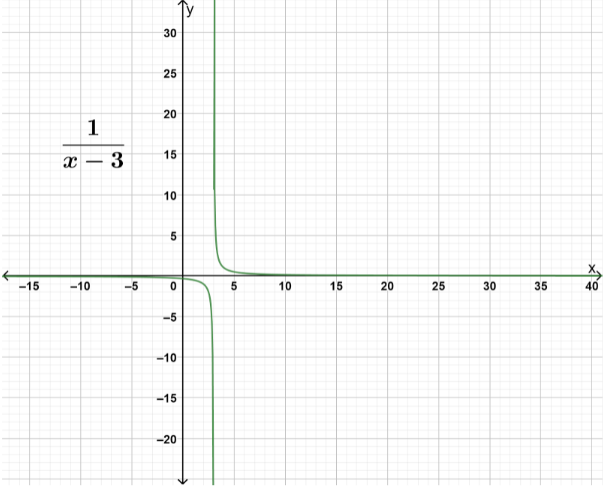
Hence, the range of the function $y = \dfrac{1}{{x - 3}}$ is all real values except zero.

Note:We must have basic knowledge about the terms domain and range. There are various methods to find the domain and range of different types of functions. In a rational function, the denominator must not be equal to zero. Also, we must know about transposition and rules of simplification in order to tackle these types of problems.