
Why does this happen? What do you see in the picture?
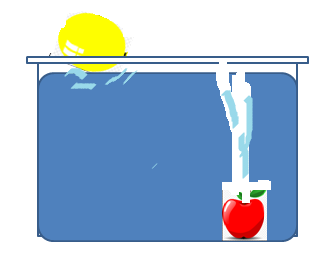

Answer
513.9k+ views
Hint: The picture has to be noticed carefully. Here it is seen the position of a balloon and an apple in a bucket full of water. Since the picture is related to the floating and sinking of objects, we have to conclude the force acting on a body in a liquid at rest. Note that the density of an object also matters for sinking or floating in liquid.
Complete answer:
When an object is left in a liquid at rest two forces act on the object simultaneously.
1)The weight of the body$({W_1})$ acts downwards normally through the center of mass.
2)The upthrust of the liquid$({W_2})$ acts upwards normally through the center of buoyancy.
If ${W_1} > {W_2}$ , i.e. the weight of the body is greater than the upthrust of the liquid, then the object sinks to the bottom of the liquid. In this case, the active downward resultant force on the object is $ = {W_1} - {W_2}$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} > {W_2} \Rightarrow {\rho _1} > {\rho _2}$
Therefore, if the density of an object is greater than the liquid in which it is immersed, the object will sink at the bottom of the liquid.
In the above picture, we can see that the apple sinks in the bottom of the bucket full of water. Hence we can say since the density of the apple is greater than the water, it sinks to the bottom of the water.
If ${W_1} < {W_2}$ , i.e. the weight of the body is less than the upthrust of the liquid, then the object floats on the surface of the liquid. In this case, the active downward resultant force on the object is $ = {W_2} - {W_1}$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} < {W_2} \Rightarrow {\rho _1} < {\rho _2}$
Therefore, if the density of an object is less than the liquid in which it is trying to be immersed, the object will not sink but float on the surface of the liquid.
In the above picture, we can see that the balloon floats on the surface of the water. Hence we can say since the density of the balloon is less than the water, it floats on the surface of the water.
Note:
There is another condition where the object can totally immerse but floats in the middle position of the container full of liquid. If ${W_1} = {W_2}$ , i.e. the weight of the body is equal to the upthrust of the liquid, then the object totally immerses and floats inside the liquid. In this case, the active downward resultant force on the object is $ = {W_2} - {W_1} = {W_1} - {W_2} = 0$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} = {W_2} \Rightarrow {\rho _1} = {\rho _2}$
Therefore, if the density of an object is equal to the liquid in which it is trying to be immersed, the object will totally immerse and float inside the liquid.
Complete answer:
When an object is left in a liquid at rest two forces act on the object simultaneously.
1)The weight of the body$({W_1})$ acts downwards normally through the center of mass.
2)The upthrust of the liquid$({W_2})$ acts upwards normally through the center of buoyancy.
If ${W_1} > {W_2}$ , i.e. the weight of the body is greater than the upthrust of the liquid, then the object sinks to the bottom of the liquid. In this case, the active downward resultant force on the object is $ = {W_1} - {W_2}$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} > {W_2} \Rightarrow {\rho _1} > {\rho _2}$
Therefore, if the density of an object is greater than the liquid in which it is immersed, the object will sink at the bottom of the liquid.

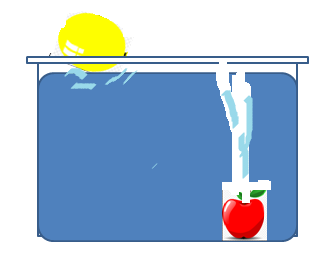
In the above picture, we can see that the apple sinks in the bottom of the bucket full of water. Hence we can say since the density of the apple is greater than the water, it sinks to the bottom of the water.
If ${W_1} < {W_2}$ , i.e. the weight of the body is less than the upthrust of the liquid, then the object floats on the surface of the liquid. In this case, the active downward resultant force on the object is $ = {W_2} - {W_1}$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} < {W_2} \Rightarrow {\rho _1} < {\rho _2}$
Therefore, if the density of an object is less than the liquid in which it is trying to be immersed, the object will not sink but float on the surface of the liquid.
In the above picture, we can see that the balloon floats on the surface of the water. Hence we can say since the density of the balloon is less than the water, it floats on the surface of the water.
Note:
There is another condition where the object can totally immerse but floats in the middle position of the container full of liquid. If ${W_1} = {W_2}$ , i.e. the weight of the body is equal to the upthrust of the liquid, then the object totally immerses and floats inside the liquid. In this case, the active downward resultant force on the object is $ = {W_2} - {W_1} = {W_1} - {W_2} = 0$.
If the density and volume of the object are ${\rho _1},{V_1}$ respectively, then ${W_1} = {\rho _1}{V_1}g$. If the density of the liquid is ${\rho _2}$, then the weight of liquid removed by the object is, ${W_2} = {\rho _2}{V_1}g$
Hence, for ${W_1} = {W_2} \Rightarrow {\rho _1} = {\rho _2}$
Therefore, if the density of an object is equal to the liquid in which it is trying to be immersed, the object will totally immerse and float inside the liquid.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




