Question

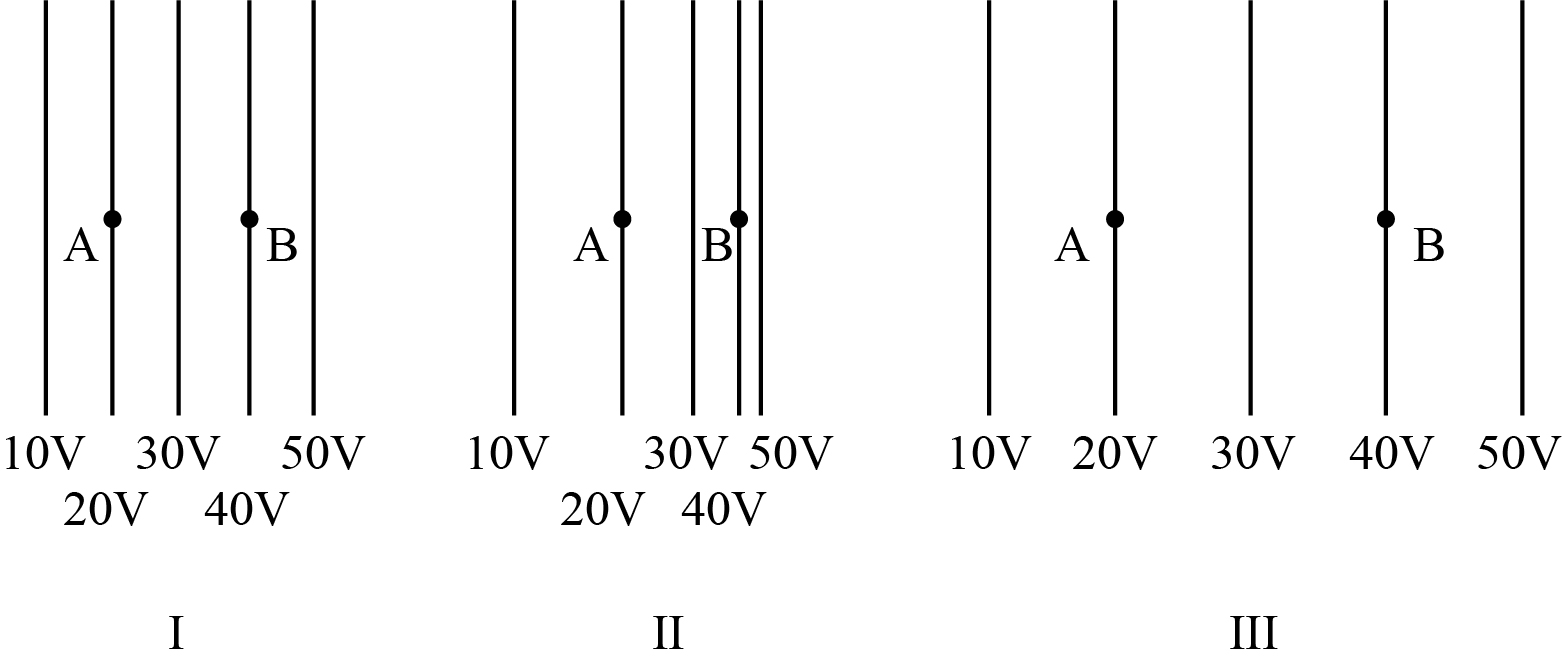
How does the magnitude of the electric field at B compare for these three cases?

A. I > III > II
B. I > II > III
C. III > I > II
D. II > I > III
E. I = II = III

Answer 1

Hint: the above problem can be resolved by using the mathematical relation of the magnitude of electric field with the electrostatic potential and the distances between the equipotential lines. Moreover, the dependency of such magnitude of the electric field with the electric potential and distance is to be analysed.
Complete step by step answer:
The mathematical relation for the electric field for the magnitude of voltage (V) through the distance (l) is given as,
\[E = - \dfrac{{dV}}{{dl}}............................\left( 1 \right)\]
This shows that the magnitude of electric field is considered as the rate of change in the electrostatic potential with the distance between the equipotential surface.
From equation 1, one can conclude that the electric field varies inversely with the distance between the equipotential surface. This implies that on increasing the distance, the magnitude of electricity increases.Thus, considering point B, it is concluded that the potential lines are closer for II and farther for III.
Hence, one can say that the magnitude of the electric field will be maximum for I and minimum for III.Therefore, the comparison for the magnitude of electric field at B is,
 II > I > III. And option D is correct.

Note: In order to resolve the given problem, one must clear with the formula of magnitude of electric field in an equipotential surface, along with the knowledge of the equipotential surfaces and corresponding equipotential lines.