
How does the force of gravitation between two objects change when the distance between them is reduced to half?
Answer
576k+ views
Hint: Gravitational force is the force of attraction between two objects having mass. Gravitational force is also called an attractive force since it always tries to attract objects together. In fact, every object in this universe has the tendency to attract other objects together, and this is due to the Universal gravitation constant. Gravitational force is directly proportional to the masses of the objects as higher the mass of the object is higher, which will be the force of gravitation.
The gravitational force between two objects is given as
\[{F_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{r^2}}}\]
Where \[{m_{_1}},{m_2}\]is the mass of the objects and \[r\]being the distance between them.
G is the universal gravitational constant which is\[ = 6.674 \times {10^{ - 11}}{m^3}.k{g^{ - 1}}.{s^{ - 2}}\]
In this question, compare the equation of the gravitational force with the force when the distance of the object is reduced.
Complete Step by Step Answer:
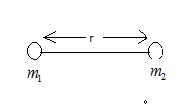
Let the masses of the two objects be \[{m_{_1}},{m_2}\]
And the distance between them \[r\]
Hence the gravitational force between them will be \[{F_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{r^2}}}\]
Now it is being said that the distance between the two objects is reduced to half as given in the figure, hence, \[r' = \dfrac{r}{2}\]
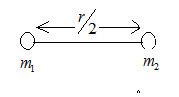
So the new gravitational force when the distance is reduced will be equal to
\[{F'_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{{\left( {r'} \right)}^2}}}\]
By substituting the new distance we get,
\[{{F'}_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} \\
= \dfrac{{G{m_{_1}}{m_2}}}{{\dfrac{{{r^2}}}{4}}} \\
= \dfrac{{4G{m_{_1}}{m_2}}}{{{r^2}}} \\
= 4{F_g} \\
\]
Hence we can conclude that if the distance between the object is halved, then the gravitational force between the object will increase four times.
Note: Students should note that gravitational force between the objects is inversely proportional to the square of their distance; hence, if the distance between objects is changed, then the force of attraction between the objects/bodies will change by multiple factors.
The gravitational force between two objects is given as
\[{F_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{r^2}}}\]
Where \[{m_{_1}},{m_2}\]is the mass of the objects and \[r\]being the distance between them.
G is the universal gravitational constant which is\[ = 6.674 \times {10^{ - 11}}{m^3}.k{g^{ - 1}}.{s^{ - 2}}\]

In this question, compare the equation of the gravitational force with the force when the distance of the object is reduced.
Complete Step by Step Answer:
Let the masses of the two objects be \[{m_{_1}},{m_2}\]
And the distance between them \[r\]
Hence the gravitational force between them will be \[{F_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{r^2}}}\]
Now it is being said that the distance between the two objects is reduced to half as given in the figure, hence, \[r' = \dfrac{r}{2}\]
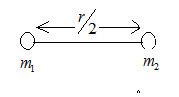
So the new gravitational force when the distance is reduced will be equal to
\[{F'_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{{\left( {r'} \right)}^2}}}\]
By substituting the new distance we get,
\[{{F'}_g} = \dfrac{{G{m_{_1}}{m_2}}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} \\
= \dfrac{{G{m_{_1}}{m_2}}}{{\dfrac{{{r^2}}}{4}}} \\
= \dfrac{{4G{m_{_1}}{m_2}}}{{{r^2}}} \\
= 4{F_g} \\
\]
Hence we can conclude that if the distance between the object is halved, then the gravitational force between the object will increase four times.
Note: Students should note that gravitational force between the objects is inversely proportional to the square of their distance; hence, if the distance between objects is changed, then the force of attraction between the objects/bodies will change by multiple factors.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




