Question

Does a median lie wholly in the interior of the triangle? (If you think this is true then draw a figure to show such a case).

Answer 1

Hint: A triangle is a 2-dimensional polygon that has three sides.

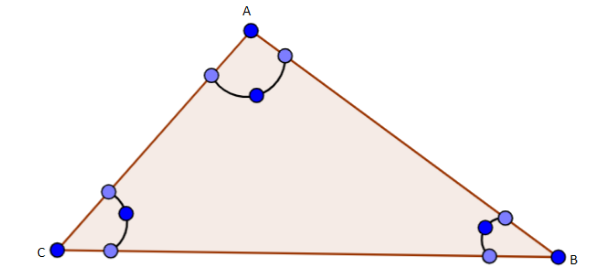
Figure: Triangle
Corners A, B, C are known as vertices of the triangle \[\vartriangle ABC\].
AB, BC, CA are the sides of the triangle \[\vartriangle ABC\].
$\angle ABC,\angle BCA,\angle CAB$ are the interior angles of the triangle \[\vartriangle ABC\], their sum is $180^\circ $, i.e.,
$\angle ABC + \angle BCA + \angle CAB = 180^\circ $
A line segment that joins the vertex of the triangle to the midpoint of the opposite side is called the median.
A triangle has three vertices and each vertex has an opposite side, thus, a triangle has three medians.
To check the given statement, draw a triangle and bisect its every side. Join the vertex and the midpoint of the opposite side i.e. median.

Complete step-by-step answer:
Step 1: Draw a triangle and bisect its one side.
To bisect the side of a triangle, you need a compass, a ruler, and a pencil.
First draw an obtuse triangle, a triangle whose one interior angle is more than ${90^ \circ }$.
Select the side which you want to bisect, here we have taken side AB.
Process 1: open the compass approximately more than the half of length of side AB. Taking vertex A as the center draws an arc, and then with the same length of the compass, taking vertex B as the center draws an arc such that it will intersect the previous arc.
Now join the vertex opposite to the side AB, i.e. vertex C and the intersection point of the arcs.
Thus the intersection point obtained on the side AB, i.e. E, is the midpoint of the side AB. And the line segment CE is the median.

Figure: Obtuse Triangle $\angle ACB > {90^ \circ }$
Step 2: Draw the median to both sides of the obtuse triangle.
Similarly, bisect the side AC and join with the vertex B, and bisect the side BC and join with the vertex A.

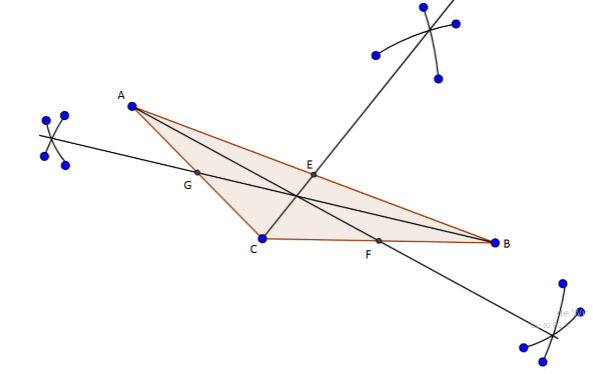
Thus, the medians of the obtuse triangle are AF, BG, CE.

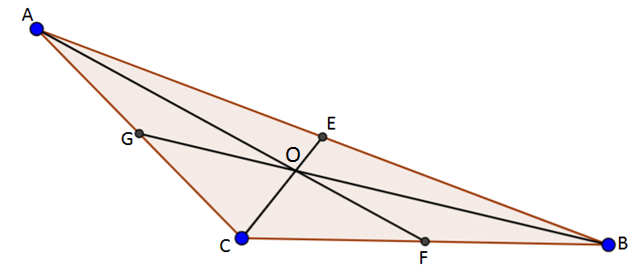
Figure: Obtuse Triangle $\angle ACB > {90^ \circ }$
Thus the medians of an obtuse triangle lie wholly inside the triangle.
Step 3: Draw the medians of a right-angled triangle.
A right-angled triangle has one interior angle exactly equal to ${90^ \circ }$.
Bisect each side, by process 1 in step 1. And join the midpoint of the side with its respective opposite vertex.
Thus the medians of a right-angled triangle are AF, BG, CE.

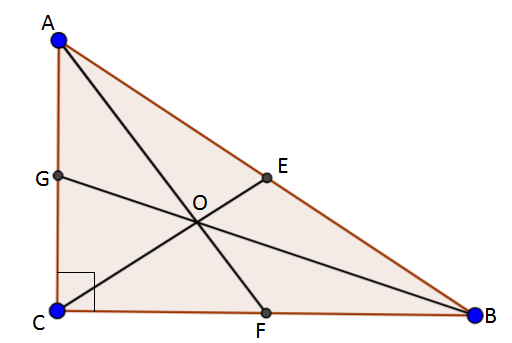
Figure: right-angled triangle $\angle ACB = {90^ \circ }$
Thus the medians of a right-angled triangle lie wholly inside the triangle.
Step 4: Draw the medians of an acute triangle.
An Acute triangle has all three interior angles less than ${90^ \circ }$.
Bisect each side, by process 1 in step 1. And join the midpoint of the side with its respective opposite vertex.
Thus the medians of an acute triangle are AF, BG, CE.
 

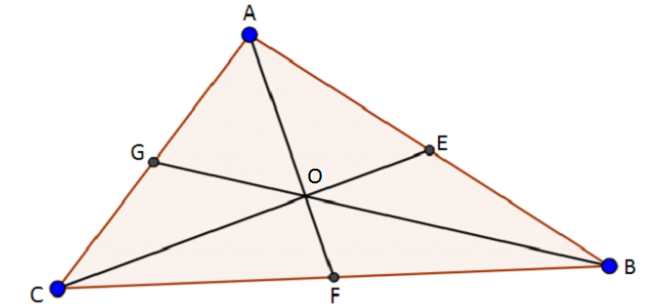
Figure: acute triangle
Thus the medians of an acute triangle lie wholly inside the triangle.

Final answer: Yes, a median lies wholly in the interior of the triangle.

Note: The intersection of the medians of a triangle called the centroid. It is represented by the point O in each triangle drawn above.
The centroid of the triangle divides each of the medians into $2:1$ ratio.
The medians of the equilateral triangle are equal in length.
An equilateral triangle has its all three sides equal in length. All three interior angles are less than ${90^ \circ }$. Thus an acute triangle.
An isosceles triangle has two sides equal in length. All three interior angles are less than ${90^ \circ }$. Thus an acute triangle.
The scalene triangle has its all three sides unequal in length. All three interior angles are less than ${90^ \circ }$. Thus an acute triangle.