Question

Divide the line segment \[PQ = 11\;cm\] in 3 equal parts.

Answer 1

Hint: A line segment is a piece or part of a line having two endpoints. Unlike a line, a line segment has a definite length and most of the shapes that we see around us are either made up of lines or curves. Various geometrical shapes are a combination of these. A one-dimensional collection of points extending infinitely in either direction is a line and any portion of a line which has two endpoints is a line segment, hence the steps are mentioned to divide the line in three equal parts.

Complete step by step solution:
 \[PQ = 11\;cm\], in which we need to divide the line in three equal parts, hence here are the following steps to divide the line segment:
Step 1: Draw a line segment PQ of length 11 cm.
Step 2: Draw an acute \[\left| \!{\underline {\,
  {CQP} \,}} \right. \]on one side of line PQ.
Step 3: Mark points Q1, Q2, Q3 on ray QC such that \[QQ1 = Q1Q2 = Q2Q3\]
Step 4: Join Q3 to P.
Step 5: Draw lines Q1 S and Q2 R parallel to Q3 P and let them intersect PQ in points S and R respectively.
Hence, points R and S divide the segment PQ in 3 equal parts.

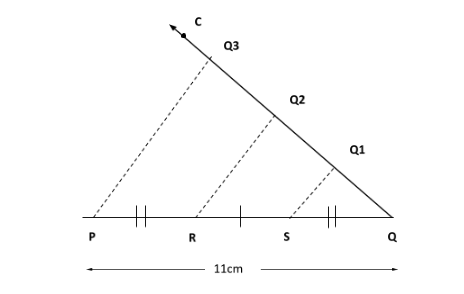
Note: Just by observing two-line segments one can predict which is long or short compared to the other. In the figure, by observation, we can say that the line segment PQ is greater in length as compared to the line segment PR and PS. But this method has several constraints, every time we cannot rely simply on observation to compare two-line segments, hence by the following steps we can divide the line segment in three equal parts.