Question

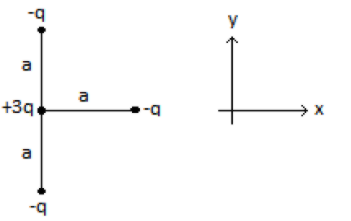
Dipole moment of the arrangement of the charges as shown in figure is

Answer 1

Hint: To solve the given question, we need to dive into the concept of dipole moment which is a quantity that describes two opposite charges separate by a small distance. The formula used to measure dipole moment is $\vec{p}=q.\vec{d}$ where $\vec{d}$ is the distance between the two charges directed from negative to positive charge and its SI unit is coulomb meter.

Complete answer:
Considering the direction in the $x-axis$ and $y-axis$ to be along positive $\hat{i}$ and $\hat{j}$
We may proceed to solve the dipole moment of each dipole to solve the question with respect to the $+3q$ charge,
Dipole moment of $-q$ along the direction of positive$y-axis$,\[{{\vec{p}}_{1}}=-q\times \vec{a}\left( {\hat{j}} \right)\]
Dipole moment of $-q$ along the direction of positive$x-axis$,\[{{\vec{p}}_{2}}=-q\times \vec{a}\left( {\hat{i}} \right)\]
Dipole moment of $-q$ along the direction of negative$y-axis$, \[{{\vec{p}}_{3}}=-q\times \vec{a}\left( -\hat{j} \right)\]
Equivalent or net dipole moment of the system,${{\vec{p}}_{net}}$ will be equal the vector sum of all the dipole moments with respect to $+3q$ charge, that is
${{\vec{p}}_{net}}={{\vec{p}}_{1}}+{{\vec{p}}_{2}}+{{\vec{p}}_{3}}$
Now, in the next step of the vector sum \[{{\vec{p}}_{1}}\] and \[{{\vec{p}}_{3}}\]would cancel each other as they have diametrically opposite directions.
$\therefore {{\vec{p}}_{net}}={{\vec{p}}_{2}}=-q\times \vec{a}\left( {\hat{i}} \right)$
Thus, the equivalent dipole moment of the system is \[-q\times \vec{a}\] along the direction of positive $x-axis$.

Note:
One is advised to always remember that dipole moments determine the direction of the charges, thus, can have both positive and negative values and if required can be resolved into its rectangular components .This again justifies that it’s a vector quantity.