Question

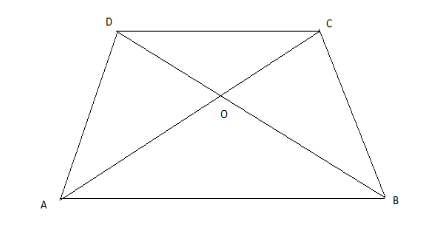
Diagonals of a trapezium \[ABCD\] with \[AB\parallel DC\], intersect each other at the point \[O\]. If \[AB = 2CD\], find the ratio of the areas of triangles \[AOB\] and \[COD\].

Answer 1

Hint: We know that; for any two right-angle triangles, if one of the other two angles is equal then the third angle is also equal to each other. This condition is known as A-A-A similarity condition. Then, we can say that the triangles are congruent.
If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides. This is known as the area of similar triangle theorems.
By using the conditions and theorem, we can find the area of the triangles.

Complete step-by-step answer:
It is given that; diagonals of a trapezium \[ABCD\] with \[AB\parallel DC\], intersect each other at the point \[O\]. Again, \[AB = 2CD\]. We have to show the ratio of the areas of triangles \[AOB\] and \[COD\].
We know that the alternate and corresponding angles of parallel lines are equal.
Since, \[AB\parallel DC\] and \[AC\& BC\] are transversal.
Then, \[\angle ODC = \angle OBA\] and \[\angle OCD = \angle OAB\] as, they are alternate angles.
In \[\Delta AOB\] and \[\Delta COD\],
\[\angle ODC = \angle OBA\] (alternate angles)
\[\angle OCD = \angle OAB\] (alternate angles)
\[\angle COD = \angle AOB\] (as they are vertically opposite angles)
So, by A-A-A condition of similarity \[\Delta AOB \cong \Delta COD\]
So, by similar triangle property we get,
\[\dfrac{{A(\Delta AOB)}}{{A(\Delta COD)}} = \dfrac{{A{B^2}}}{{C{D^2}}}\]
We have, \[AB = 2CD\]
Substitute this relation above equation we get,
\[\dfrac{{A(\Delta AOB)}}{{A(\Delta COD)}} = \dfrac{{{{(2CD)}^2}}}{{C{D^2}}}\]
Simplifying we get,
\[\dfrac{{A(\Delta AOB)}}{{A(\Delta COD)}} = \dfrac{4}{1}\]
Hence, \[A(\Delta AOB):A(\Delta COD) = 4:1\]

Hence, the ratio of the areas of triangles \[AOB\] and \[COD\] is \[4:1.\].

Note: If, the three angles of any triangle are equal to the respective angles of another triangle, then the triangle is called a congruence triangle. This condition is known as A-A-A condition.
We know that the alternate and corresponding angles of parallel lines are equal.
If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides. This is known as the area of similar triangle theorems.