
How do you determine whether each function represents exponential growth or decay $y=3{{\left( \dfrac{5}{2} \right)}^{x}}$ ?
Answer
541.2k+ views
Hint:
In this problem we have found the exponential growth or decay of the given expression that is $y=3{{\left( \dfrac{5}{2} \right)}^{x}}$. First, we want to check whether the given expression is exponential form or not. The general form of the exponential function is $y=a{{b}^{x}}$. Now we will compare the given equation with the standard equation and we will write the values of $a$, $b$. Now from the values of the $a$ and $b$ we will decide whether the given equation is exponential decay or growth. If the value of $a$ is positive and the value $b$ is greater than $1$ then we can call it as exponential growth and if the value of $a$ is positive and $b$ is less than $1$ then we can call it as exponential decay.
FORMULA USE:
exponential function form of $y=a{{b}^{x}}$.
Complete step by step solution:
Given that, $y=3{{\left( \dfrac{5}{2} \right)}^{x}}$.
To whether the given equation is in exponential form or not. We are going to check whether the given equation is the form of $y=a{{b}^{x}}$. By observing the given equation, we can say that the given equation is an exponential function and the values of $a$, $b$ are
$a=3$ , $b=\dfrac{5}{2}$
In the given equation we have the value of $a$ as the positive. Considering the value of $b$ . We have $b=\dfrac{5}{2}$ which is greater than $1$. So, we can say that the given exponential equation has growth.
Note:
We can also plot the graph and see the growth of the given equation. The graph of the given equation is
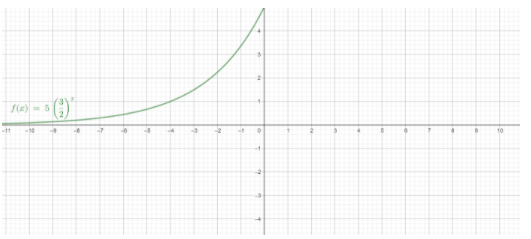
In this problem we have found the exponential growth or decay of the given expression that is $y=3{{\left( \dfrac{5}{2} \right)}^{x}}$. First, we want to check whether the given expression is exponential form or not. The general form of the exponential function is $y=a{{b}^{x}}$. Now we will compare the given equation with the standard equation and we will write the values of $a$, $b$. Now from the values of the $a$ and $b$ we will decide whether the given equation is exponential decay or growth. If the value of $a$ is positive and the value $b$ is greater than $1$ then we can call it as exponential growth and if the value of $a$ is positive and $b$ is less than $1$ then we can call it as exponential decay.
FORMULA USE:
exponential function form of $y=a{{b}^{x}}$.
Complete step by step solution:
Given that, $y=3{{\left( \dfrac{5}{2} \right)}^{x}}$.
To whether the given equation is in exponential form or not. We are going to check whether the given equation is the form of $y=a{{b}^{x}}$. By observing the given equation, we can say that the given equation is an exponential function and the values of $a$, $b$ are
$a=3$ , $b=\dfrac{5}{2}$
In the given equation we have the value of $a$ as the positive. Considering the value of $b$ . We have $b=\dfrac{5}{2}$ which is greater than $1$. So, we can say that the given exponential equation has growth.
Note:
We can also plot the graph and see the growth of the given equation. The graph of the given equation is

Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Which one of the following groups comprises states class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

A couple went for a picnic They have 5 sons and each class 8 maths CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE





