Question

How do you determine the vector and parametric equations for the plane through point (1 -2, 3) and parallel to the xy-plane?

Answer 1

Hint: To determine the vector and parametric equation for the plane we should check the conditions given in the question. It is mentioned that it is parallel to the xy plane. So it means the plane is perpendicular to the z axis then from this condition we find the value of the z coordinate in the given point. Then we represent it in required forms.

Complete step by step solution:
Any plane that is parallel to the xy - plane is perpendicular the the z-axis. i.e. it has a normal vector given by:
\[\overrightarrow{n}=\left. \left( \begin{matrix}
0 \\
0 \\
1 \\
\end{matrix} \right. \right)\]
Hence the plane has an equation of the form:
0x + 0y + 1z = k
\[\Rightarrow \] z = k
We want the plane to pass through (1, −2, 3) and so the value of k becomes 3 So, k = 3
Hence the required plane equation is
z = 3
For the vector equation we use the form as given below:
\[\left( \overrightarrow{r}-\overrightarrow{{{r}_{0}}} \right).\overrightarrow{n}=0\]
\[\Rightarrow \overrightarrow{r}.\overrightarrow{n}=\overrightarrow{{{r}_{0}}}.\overrightarrow{n}\]
This gives us the equation as below:
\[\Rightarrow \overrightarrow{r}.\left. \left( \begin{matrix}
0 \\
0 \\
1 \\
\end{matrix} \right. \right)=\left. \left( \begin{matrix}
1 \\
-2 \\
3 \\
\end{matrix} \right. \right).\left. \left( \begin{matrix}
0 \\
0 \\
1 \\
\end{matrix} \right. \right)\]
\[\Rightarrow \overrightarrow{r}.\left. \left( \begin{matrix}
0 \\
0 \\
1 \\
\end{matrix} \right. \right)=\] 3
We can show this equation obtained on a 3D plot as follows:

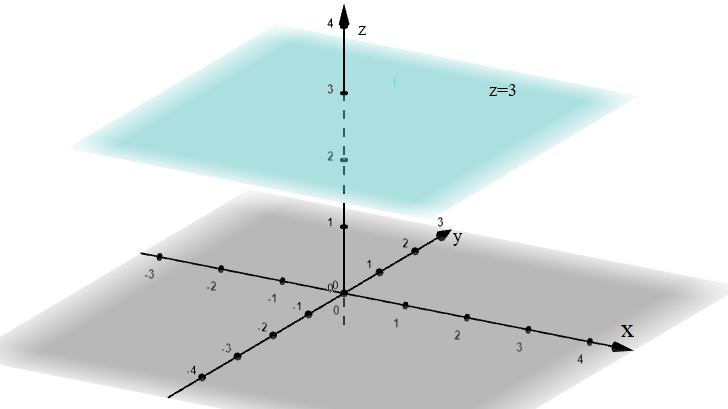
Note: It is required to know the procedure to be followed in solving these kinds of questions. We have to be well versed in converting the equation of the plane obtained in vector form and then we can plot the graph according to the obtained solution.