Question

Determine the electric potential at point P due to two point charges each of charge $+Q$ with one point charge being at a distance $R$ and other being at a distance $2R$.

Answer 1

Hint: Due to the electrostatic forces acting between the charges, there is some potential acting on a charge in the field of another charge. The work done to move a charge from one point to the other in a field is called electric potential difference between two points in the field. Potential has a direct relation to the product of charges and inverse relation to the distance between them.

Formulas used:
$P=\dfrac{{{Q}_{1}}{{Q}_{2}}}{4\pi {{\varepsilon }_{0}}r}$

Complete step-by-step solution:
The potential difference due a charged particle is defined as the work done to move another charged particle between two points. Positive potential is due to a positive charge and negative potential is due to a negative charge.
It is given as-
$P=\dfrac{{{Q}_{1}}{{Q}_{2}}}{4\pi {{\varepsilon }_{0}}r}$ - (1)
Here,
$P$ is the potential difference
${{Q}_{1}},\,{{Q}_{2}}$ are charges on the charged particles
$r$ is the distance between the particles
${{\varepsilon }_{0}}$ is the permeability of free space

Given potential at point P is influenced by two charges having charge $+Q$ each, at a distance of $R$ and $2R$ respectively.

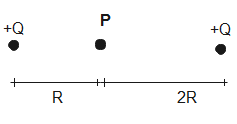
Therefore, potential at point P will be due to both charges.

We substitute given values in eq (1) to get,
$\begin{align}
  & P={{P}_{1}}+{{P}_{2}} \\
 & \Rightarrow P=\dfrac{{{Q}_{1}}}{4\pi {{\varepsilon }_{0}}{{R}_{1}}}+\dfrac{{{Q}_{2}}}{4\pi {{\varepsilon }_{0}}{{R}_{2}}} \\
 & \Rightarrow P=\dfrac{Q}{4\pi {{\varepsilon }_{0}}R}+\dfrac{Q}{4\pi {{\varepsilon }_{0}}2R} \\
 & \therefore P=\dfrac{3Q}{8\pi {{\varepsilon }_{0}}R} \\
\end{align}$

Therefore, the potential at point P due to both charges is$\dfrac{3Q}{8\pi {{\varepsilon }_{0}}R}$.

Note:
A unit charge is assumed to be kept at point P on which potential due to the charges is acting on. When the work is done to bring a unit charge from infinity to a point, then it is called electric field. Positive charge has a tendency to flow from higher electric potential to lower electric potential. According to coulomb’s law, electrostatic force has a direct relation to the product of charges and inverse relation to the square of distance between them.