Question

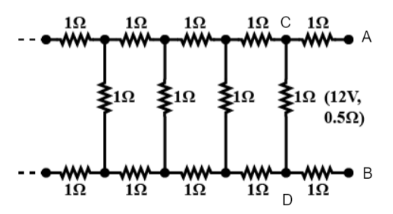
Determine the current drawn from a \[12{\text{ V}}\]supply with internal resistance \[{\text{0}}{\text{.5 }}\Omega \] by the infinite network as shown in the figure. Each resistor has \[{\text{1 }}\Omega \] resistance

Answer 1

Hint: In this question, there are infinitely long strings of \[{\text{1 }}\Omega \] resistors, and let us assume the resistance of the infinitely long combination be \[R{\text{ }}\Omega \]. Even if we detach the first three resistors from the front section there will not be any effect on the resistance of the combination. Thus, the resistance of combination across C and D will be the same as that of resistance across A and B and will be equal to \[R\]. Then we can use the parallel and series resistance formula to find \[R\] and then add the internal resistance of the battery and use ohm’s law to find out the current drawn from \[12{\text{ V}}\] supply.

Formula used:
Ohm’s law: \[V = IR\]
Equivalent resistance for resistor in series: \[{R_{eq}} = {R_1} + {R_2}\]
Equivalent resistance for resistors in parallel: \[\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]

Complete step by step answer:
Given in the question there are infinitely long string of \[{\text{1 }}\Omega \] resistors connected to a battery of \[12{\text{ V}}\]and \[{\text{ 0}}{\text{.5 }}\Omega \] internal resistance.We need to find the current drawn from the battery.Let us assume the equivalent resistance of an infinite long combination of resistors across A and B be \[R{\text{ }}\Omega \].

Now as we are having the infinite number of resistors, we detach the first three resistors from the front section of it as shown in the below diagram, and the resistance of the part to the left of C and D will be the same as the resistance between A and B. So, we can consider the part on the left of C and D has a resistance \[R\] and is connected in parallel with a \[{\text{ 1 }}\Omega \] resistor and the combination of these are in series with two \[{\text{ 1 }}\Omega \] resistors.

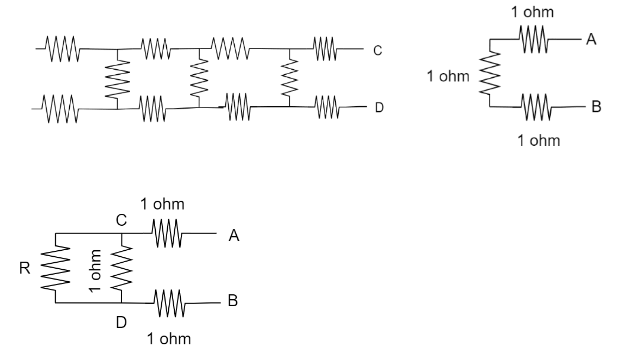
Let Resistance across C and D be \[{R_1}\]
\[\dfrac{1}{{{R_1}}} = \dfrac{1}{R} + \dfrac{1}{1}\]
\[ \Rightarrow \dfrac{1}{{{R_1}}} = \dfrac{{R + 1}}{R}\]
\[ \Rightarrow {R_1} = \dfrac{R}{{R + 1}}\]
Resistance across A and B is \[{R_1} + 1 + 1\]

But we know resistance across A and B is \[R{\text{ }}\Omega \].
Therefore,
\[R = {R_1} + 1 + 1\]
\[ \Rightarrow R = \dfrac{R}{{R + 1}} + 1 + 1\]
\[ \Rightarrow R = \dfrac{R}{{R + 1}} + 2\]
Multiplying both sides with \[\left( {R + 1} \right)\] we get,
\[R \times \left( {R + 1} \right) = R + 2\left( {R + 1} \right)\]
\[ \Rightarrow {R^2} + R = 3R + 2\]
\[ \Rightarrow {R^2} - 2R - 2 = 0\]

On solving the quadratic equation, we get,
\[ \Rightarrow R = \dfrac{{2 \pm \sqrt {{2^2} + 4 \times 2} }}{2}\]
\[ \Rightarrow R = \dfrac{{2 \pm \sqrt {12} }}{2}\]
\[ \Rightarrow R = 1 \pm \sqrt 3 \]
But resistance cannot be negative
\[R \ne 1 - \sqrt 3 \]
Therefore \[R = 1 + \sqrt 3 {\text{ }}\Omega \]
\[R = 2.732{\text{ }}\Omega \]
Total resistance of the circuit is \[R + 0.5 \Rightarrow 2.732 + 0.5 \Rightarrow 3.232{\text{ }}\Omega \]
Current drawn from \[12{\text{ V}}\] supply is,
\[I = \dfrac{V}{R} \\
\Rightarrow I= \dfrac{{12}}{{3.232}} \\
\therefore I= 3.7{\text{ }}A\]

Hence, the current drawn from a \[12{\text{ V}}\] supply with internal resistance \[{\text{0}}{\text{.5 }}\Omega \] by the infinite network is 3.7 A.

Note: The resistance of the infinite ladder and part of the infinite ladder is the same because there are infinite resistances so detaching some of the resistors won’t affect the resistance of the ladder. On solving we will get a quadratic equation and one value of resistance will be negative which must be rejected.