Question

Determine the coordinates of image location for objects kept at origin as shown in figure.
 

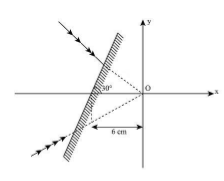
Answer 1

Hint:For the determination of the coordinates of the image location first, we will draw the diagram of the image location with the help of concepts related to the mirror. After drawing the diagram, we will use trigonometry for the calculation of the required coordinates.

Complete step by step answer:
We know that the formation of image and position of the object are on the opposite sides of the mirror, but at the same normal and at the equal distance, so according to this
information we will draw the diagram to represent the location of the image.

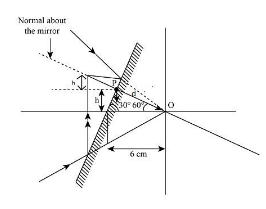
In the above diagram, we can see that the mirror makes $30^\circ $ with the x axis and the normal makes $60^\circ $ with the x-axis, so will use trigonometry for the determination of the required coordinates.
Therefore, we get
$
\sin 30^\circ = \dfrac{d}{{6\;{\rm{cm}}}}\\
d = \sin 30^\circ \times 6\;{\rm{cm}}
$
Here $d$ is the x coordinate of the image and put $\sin 30^\circ = 0.5$ in the above equation, so
$
d = 0.5 \times 6\;{\rm{cm}}\\
d = 3\;{\rm{cm}}
$
Here the height above and below the point P is almost the same so that we will use the values of x coordinate, and the angle made by normal with x-axis for the calculation of the Y co-ordinate of the image.
Therefore, we get
$
\sin 60^\circ = \dfrac{{2h}}{d}\\
2h = \sin 60^\circ \times d
$
Let $2h = H$ is the Y coordinate of the image, so the above equation becomes
$H = \sin 60^\circ \times d$
Substitute $d = 3\;{\rm{cm}}$ and $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$ in the above equation, therefore we get
$
H = \dfrac{{\sqrt 3 }}{2} \times 3\;{\rm{cm}}\\
H = 2.6\;{\rm{cm}}
$
Therefore, the coordinates of the image location for objects kept at origin are $\left( {3\;{\rm{cm,}}\;2.6\;{\rm{cm}}} \right)$.

Note: During calculation, make sure that you are putting write values of the \[\sin 30^\circ \] and $\sin 60^\circ $, so that you can obtain the correct calculation. So, clear the concept of trigonometry for these types of questions. If you put the wrong values of $\sin 60^\circ $ and \[\sin 30^\circ \], the final answer may vary.