Question

How do you determine the area to the left of $g\left( y \right)=3-{{y}^{2}}$ and to the right of $x=-1$ ?

Answer 1

Hint: We have been given two functions and we have to find the area enclosed by those functions. The left boundary of the area enclosed is $x=-1$ and the area is contained by the function $g\left( y \right)=3-{{y}^{2}}$. We shall first plot these two functions on the same cartesian plane and find their two points of intersections. Then we shall perform definite integration on the function $g\left( y \right)=3-{{y}^{2}}$ taking the two points of intersections as the limits.

Complete step-by-step solution:
Given are two functions $g\left( y \right)=3-{{y}^{2}}$ and $x=-1$ where one function is straight-line parallel to the y-axis and the other function is parabolic in nature.

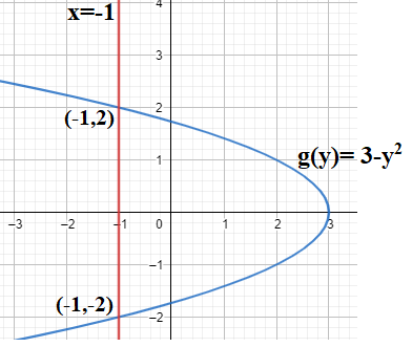
Here, we see that the points of intersection of these two functions are $\left( -1,2 \right)$ and $\left( -1,-2 \right)$.
Thus, the required region is the shaded region in the graph below.

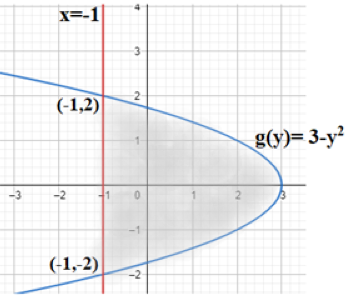
In order to find the enclosed area, we shall integrate $g\left( y \right)=3-{{y}^{2}}$ from $y=2$ to $y=-2$.
$A=\int\limits_{-2}^{2}{3-{{y}^{2}}.dy}$
From the basic properties of integration, we know that $\int{3.dy=3y}+C$ and $\int{{{y}^{n}}.dy=\dfrac{{{y}^{n+1}}}{n+1}}+C$. We shall use these properties to integrate our function.
 $\Rightarrow A=\left. 3y-\dfrac{{{y}^{3}}}{3} \right|_{-2}^{2}$
Now, we will apply the upper limit of the integral equal to 2 and the lower limit of the integral equal to -2.
$\Rightarrow A=3\left( 2 \right)-\dfrac{{{\left( 2 \right)}^{3}}}{3}-\left( 3\left( -2 \right)-\dfrac{{{\left( -2 \right)}^{3}}}{3} \right)$
Since ${{2}^{3}}=2\times 2\times 2=8$, thus substituting ${{2}^{3}}=8$, we get
$\Rightarrow A=6-\dfrac{8}{3}-\left( -6-\dfrac{\left( -8 \right)}{3} \right)$
$\Rightarrow A=6-\dfrac{8}{3}+6-\dfrac{8}{3}$
$\Rightarrow A=12-\dfrac{16}{3}$
$\Rightarrow A=\dfrac{20}{3}$
Therefore, the area to the left of $g\left( y \right)=3-{{y}^{2}}$ and to the right of $x=-1$ is $\dfrac{20}{3}$ square units.

Note: Definite integral of a function $f\left( y \right)$ is the area bound under the graph of function, $x=f\left( y \right)$and above the y-axis which is bound between two bounds as $y=a$ and $y=b$. Here, $a=$ -2 and $b=$2. The best thing about integral calculus is that the one of the two boundaries of the area to be found is a curve and the other boundary is the y-axis when the function is being integrated with respect to $dy$.