Question

Describe the experiment to compare the E.M.F.’s of two cells by potentiometer under the following headings:
A). Circuit diagram
B). Formula
C). Observation table
D). Two precautions

Answer 1

Hint: The possible gap between a cell's two terminals can be calculated using a voltmeter, but we can calculate the emf value of a given cell using a potentiometer. Where ${E_1}$ and ${E_2}$ are two-cell EMFs, ${l_1}$ and ${l_2}$ are the lengths for balancing while ${E_1}$ and ${E_2}$, respectively, are attached to the circuit and $\rho $ the potential gradient along the wire of the potentiometer.

Complete step-by-step solution -
Part-A

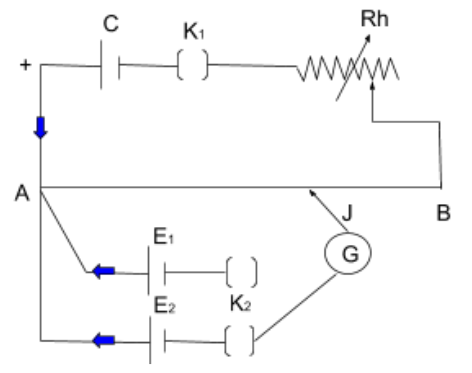
${K_1}$ is the Plug key
${K_2}$ is the Two-way key
$R_h$ is the Rheostat
$J$ is the Jockey
$AB$ is the Potentiometer wire
$G$ is the Galvanometer
${E_1},{E_2}$ are the Experimental/Sample cells
$C$ is the Lead cell
Part-B
Formula:
Let’s consider ${E_1}$ to be the E.M.F. of the first cell.
Let the balancing point that was obtained be at a distance of ${l_1}$. Applying the rule of the principle of potentiometer, we will get-
$ \Rightarrow {E_1} = \rho {l_1}$
Let the above equation be equation 1.
$ \Rightarrow {E_1} = \rho {l_1}$ (equation 1)
Let’s consider ${E_2}$ to be the E.M.F. of the second cell. Let the balancing point be obtained at a distance of ${l_2}$. Thus-
$ \Rightarrow {E_2} = \rho {l_2}$
Let this equation be equation 2.
$ \Rightarrow {E_2} = \rho {l_2}$ (equation 2)
Now, we will divide equation 2 by equation 1, we get-
$ \Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{\rho {l_1}}}{{\rho {l_2}}} = \dfrac{{{l_1}}}{{{l_2}}}$
Part-C
Observation:
We will observe that the length of the null point for $\left( {\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{l_1}}}{{{l_2}}}} \right)$.
${E_1} = {l_1}cm$
${E_2} = {l_2}cm$
Part-D
Precautions:
E.M.F. would be greater than the sample cell of the lead cell.
Each positive terminal should always be connected to only one point.

Note: A potentiometer makes an adjustable voltage divider using a three-terminal resistor with a slipping and rotational contact. It functions as a variable resistor or rheostat if only two terminals are used: one end and the wiper. The measurement device known as potentiometer is simply a voltage divider used to calculate strength (voltage); the variable has the same concept and thus the name of the measuring instrument.