Question

Derive the relationship between the focal length and radius of curvature of a spherical mirror.

Answer 1

Hint: A spherical mirror is a part of an imaginary sphere. The radius of this imaginary sphere is called the radius of curvature. The focus of the spherical mirrors is the point where all parallel rays meet or seem to meet after reflection.

Complete step by step solution:
Light rays parallel to the main axis of a concave mirror tend to align right between the centre and the centre of the mirror on a point opposite the Spiegel. That makes it a converging mirror, which is called a focal point or focus where the rays converge. It is possible to illustrate that the emphasis is roughly halfway between the middle and poles with a bit of geometry (and a lot of simplicity).

Positions in the sphere around a spherical mirror like the axis of a coordinate system are defined by the main axis. The pole is the source. Positive coordinate values are assigned to the positions in front of a spherical mirror. The ones behind, evil. Those behind. The radius of curvature is considered the distance from the pole to the origin of the curvature. Focal length is defined as the distance from the pole to the focus. A spherical mirror's focal length is then almost half the curvature radius.

Proof- Consider a light beam, AB and the incidence on a spherical mirror at point B in accordance with the main axis. The radius of curvature is the normal on the surface at B and \[CP {\text { }} = {\text { }} CB {\text { }} = {\text { }} R\]. The ray AB moves through the mirror F (concave mirror) or tends to be distinct from F (convex mirror) after reflection and complies with the law of reflection which is angle of incidence $i$ is equal to angle of reflection $r$ , $i = r$.

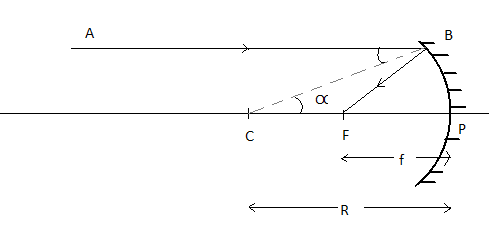
Now, according to the given figure,
\[\angle {\text { }} i = \angle \alpha \] (Alternate Angles)
Therefore,
\[\angle {\text{r}} = \angle \alpha \]
Now, in triangle BCF,
$CF = FB$
Therefore, triangle BCF is an isosceles triangle.
Considering that the aperture of the mirror is small, B and F are close to each other, therefore, we can write that,
$FB \simeq FP$
Therefore, from the above equations,
$FP = CF = \dfrac{1}{2}CP$
Now,
$CP = R$ and $PF = f$
Therefore,
$f = \dfrac{R}{2}$
Hence the above given equation is the relationship between the focal length and radius of curvature of a spherical mirror. The principle focus lies midway of the radius of curvature of the spherical mirror.

Note: The given result and relation between focal length and radius of curvature of a spherical mirror is approximately true as the point B and F are considered to be at the same point since we assume that the aperture of the mirror is very small.