Question

Derive the lens maker's formula.

Answer 1

Hint: Consider a double convex lens and a point object is located on the principal axis and the ray incident on the first spherical surface and it gets refracted.

Complete step by step answer:
Lens maker’s formula relates the focal length of a lens to the refractive index of the lens material and the radii of curvature of its two surfaces. For second refraction, the image of first reflection becomes the object of second refraction.
The figure below represents the refraction through a double convex lens:

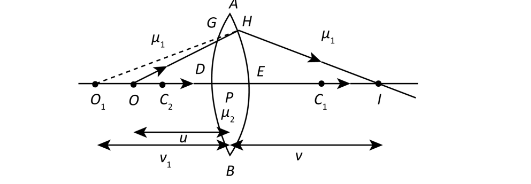
Here, ${C_1}$ and ${C_2}$ are the centres of curvature of two spherical surfaces of the convex
lens. $O$ represents an object and ${O_1}$ is the image due to first refraction. The refractive
The index of the medium is ${\mu _1}$ and the refraction index of the lens is ${\mu _2}$.
Let us consider the radii of the curvature be ${R_1}$ and ${R_2}$.
Using the formula for refraction at a curved surface, for the first time refraction at $ADB$,
image distance is ${v_1}$, we have,
$\dfrac{{{\mu _2}}}{{{v_1}}} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{{{R_1}}}$... (I)
The final image $I$, which is an image due to second refraction as well.
Now we know for the second refraction, ${v_1}$ becomes the object distance.
$\dfrac{{{\mu _1}}}{v} - \dfrac{{{\mu _2}}}{{{v_1}}} = \dfrac{{{\mu _1} - {\mu _2}}}{{{R_2}}}$... (II)

Now we add equation (I) and (II), we have,

$

\dfrac{{{\mu _1}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{{{R_1}}} +
\dfrac{{{\mu _1} - {\mu _2}}}{{{R_1}}}\\
{\mu _1}\left( {\dfrac{1}{v} - \dfrac{1}{u}} \right) = \left( {{\mu _2} - {\mu _1}} \right)\left(
{\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)\\
\left( {\dfrac{1}{v} - \dfrac{1}{u}} \right) = \left( {\dfrac{{{\mu _2}}}{{{\mu _1}}} - 1} \right)\left(
{\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)
$
If the object is placed at infinity $\left( {u = \infty } \right)$, the image will be formed at the
focus, $v = f$. Thus, the above equation becomes,
$\dfrac{1}{f} = \left( {\dfrac{{{\mu _2}}}{{{\mu _1}}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} -
\dfrac{1}{{{R_2}}}} \right)$

This is known as Lens maker’s formula.

Note: The assumptions made in the derivation of the formula:
1. The object is a point object located on the principal axis.
2. The aperture of the lens is small.
3. All the rays make very small angles with the normal to the lens faces.
4. The lens is thin.