Question

Derive the expression for voltage gain of a transistor amplifier in CE configuration terms of the load resistance ${R_L}$, current gain ${\beta _\alpha }$ and input resistance. Explain why input and output voltages are in opposite phases.

Answer 1

Hint: Here, we will use Kirchhoff’s law to derive the expression for a voltage gain of a transistor amplifier in CE configuration. Also, keep in mind that an amplifier is a device that is used to increase the amplitude of the input signal.

Complete step by step solution:
As we know, the operation of a transistor as an amplifier is possible only if we fix its operating point in the middle of its active region.

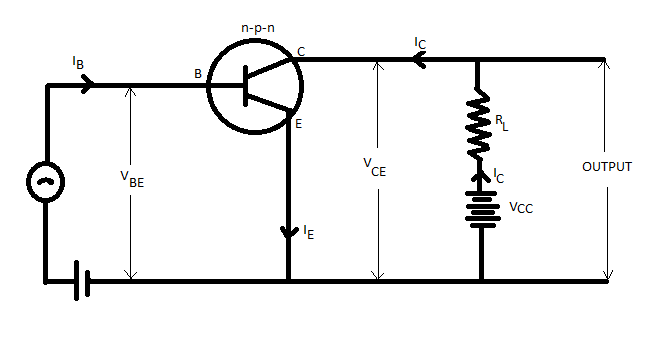
Now, we all know that amplifiers are used to amplify the alternating signals. Therefore, we will superimpose the ac input signal ${v_i}$ on ${v_{BB}}$. The output will be taken between the collector and ground.
Now, for an amplifier, we will take ${v_i} = 0$.
Hence, using Kirchhoff’s law to the output loop, we get
${V_{CC}} = {V_{CE}} + {I_C}{R_L}$
Now, using Kirchhoff’s law to the input loop, we get
${V_{BB}} = {V_{BE}} + {I_B}{R_B}$
Here, when ${V_i}$ is not zero, we get
${V_{BB}} + {v_i} = \left( {{V_{BE}} + \Delta {V_{BE}}} \right) + \left( {{I_B} + \Delta {I_B}} \right){R_B}$
Or ${V_{BB}} + {v_i} = {V_{BE}} + {I_B}{R_B} + \Delta {V_{BE}} + \Delta {I_B}{R_B}$
Here, the change in ${V_{BE}}$ can be related to the input resistance ${r_i}$ and the change in ${I_B}$ is given by
$\Delta {V_{BE}} = \Delta {I_B}{r_i}$
So, we will get
${V_{BB}} + {v_i} = {V_{BE}} + {I_B}{R_B} + \Delta {I_B}({R_B} + {r_i})$
Now, we will get the value of ${v_i}$ as
${V_{BB}} + {v_i} - {V_{BB}} = {V_{BE}} + {I_B}{R_B} + \Delta {I_B}({R_B} + {r_i}) - {V_{BE}} - {I_B}{R_B}$
$ \Rightarrow \,{v_i} = \Delta {I_B}({R_B} + {r_i})$
$ \Rightarrow \,{v_i} = r\Delta {I_B}$

Now, we can say that a change in ${I_B}$ causes a change in ${I_C}$. Therefore, we define will a new parameter ${\beta _{ac}}$ which is also similar to ${\beta _{dc}}$, as
${\beta _{ac}} = \dfrac{{\Delta {I_C}}}{{\Delta {I_B}}} = \dfrac{{{i_C}}}{{{i_B}}}$
This equation is also known as the current gain ${A_i}$. Usually, ${\beta _{ac}}$ remains close to ${\beta _{dc}}$ in the linear region of the output characteristics. Now, the change in ${I_C}$due to a change in ${I_B}$ leads to the change in ${V_{CE}}$ and the voltage drop across the resistor ${R_L}$, because ${V_{CC}}$ is fixed.

We can see the changes in the equation given below
$\Delta {V_{CC}} = \Delta {V_{CE}} + {R_L}\Delta {I_C}$
Here, if we consider $\Delta {V_{CC}} = 0$,
 $\therefore \,\Delta {V_{CE}} = - {R_L}\Delta {I_C}$
Now, we know ${\beta _{ac}} = \dfrac{{\Delta {I_C}}}{{\Delta {I_B}}}$
Therefore, value of $\Delta {I_C}$from this equation to the above equation, we get
${v_0} = \Delta {V_{CE}} = - {\beta _{ac}}{R_L}\Delta {I_B}$
Therefore the voltage in the amplifier is given by
${A_v} = \dfrac{{{v_0}}}{{{v_i}}}$
$ \Rightarrow {A_v} = \dfrac{{\Delta {V_{CE}}}}{{r\Delta {I_B}}}$
$ \Rightarrow {A_v} = \dfrac{{ - {\beta _{ac}}{R_L}}}{r}$

Here, the negative sign shows that the output voltage is in the opposite phase to the input voltage.

Note: Consider that we apply an input signal voltage ${V_i}$ to the emitter-base circuit. We will observe that there will be a change in base current and collector current respectively.
Also, when the input voltage increases, the current through the base-circuit also increases. This will lead to a fall in the voltage between the collector and emitter terminals.