Question

Derive the expression for the intensity of magnetic field at a point in end on position due to a short bar magnet.

Answer 1

Hint:To solve the this question first of all we have to understand what is end on position for the short bar magnet and then after we will derive the expression for magnetic field due to north and south pole of the bar magnet separately by using the formula: \[B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{x^2}}}\], where m is pole strength, x is the distance from the centre of the bar magnet and B is the intensity of magnetic field. In order to get the required expression we will finally calculate the resultant magnetic field due to both north and south poles at particular locations in the end on position.

Complete step-by-step answer:
Let Q be a point in end on position (It is a position lying on the magnet axis of the bar magnet) at a distance x from the centre of the short bar magnet with magnetic length 2L.
We consider NS is a short bar magnet with magnetic length 2L and pole strength m such that \[\left( {L < < x} \right)\] as shown below.

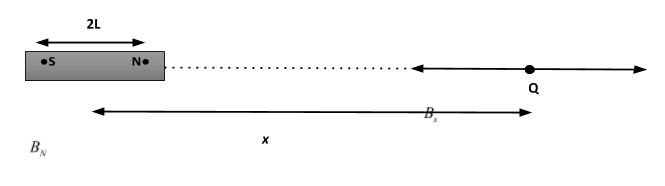
Now, the magnetic field at point Q due to north-pole is:-
 \[{B_N} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{(x - L)}^2}}}\], with its direction is away from the magnet.
Similarly, the magnetic field at point Q due to south-pole is:-
\[{B_s} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{(x + L)}^2}}}\], with its direction is towards the magnet.
The Resultant magnetic field at the point Q is:
\[{\vec B_R} = {\vec B_s} + {\vec B_N}\]
Since,\[{\vec B_N}\] and \[{\vec B_s}\] are opposite in direction as shown in the above diagram.
So, Magnitude of the resultant magnetic field is written as:
\[{B_R} = {B_N} - {B_s}\]…………… (i)
Substitute the values of \[{B_N}\]and \[{B_s}\]in the eqn (i), we get:
\[{B_R} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{(x - L)}^2}}} - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{{(x + L)}^2}}}\]
      \[ = \dfrac{{{\mu _0}m}}{{4\pi }}\left[ {\dfrac{1}{{{{(x - L)}^2}}} - \dfrac{1}{{{{(x + L)}^2}}}} \right]\]
\[ \Rightarrow {B_R} = \dfrac{{{\mu _0}m}}{{4\pi }}\left[ {\dfrac{{4Lx}}{{{{({x^2} - {L^2})}^2}}}} \right]\]
Hence, the expression of magnitude for the intensity of magnetic field in end on position is
\[ \Rightarrow {B_R} = \dfrac{{{\mu _0}m}}{{4\pi }}\dfrac{{4Lx}}{{{{({x^2} - {L^2})}^2}}}\]
 We can also write it in the term of magnetic moment of the bar magnet as:
\[ \Rightarrow {B_R} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2Mx}}{{{{({x^2} - {L^2})}^2}}}\]………… (ii) [Where we take\[\left( {M = 2mL} \right)\]which is the magnetic moment of the bar magnet.]
Applying small-size approximation in eqn (ii)
Since, \[\left( {L < < x} \right)\] therefore we can ignore L in the equation (ii), we get
\[ \Rightarrow {B_R} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2Mx}}{{{{({x^2})}^2}}}\]
           \[ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{x^3}}}\]
Hence, the Intensity of magnetic field for short size bar magnet at the end-on position is expressed as:
\[{B_R} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{x^3}}}\]

Note:It is recommended that students do not get confused with the term Intensity of magnetic field with some other physical entity. One should also understand the meaning of the end-on and Broadside-on position. The magnetic field intensity will be the same for all the infinitesimal elements.