Question

Derive the expression for capacitance of parallel plate capacitor.

Answer 1

Hint: For a parallel plate capacitor charge density is opposite for both the plates. And the electric field between the plates is directed from positive to negatively charged plate. This electric field will give the value of potential difference between the plates. Use that to find the capacitance.

Formula Used:
Electric field at a point in front of an infinite charged sheet is:
$E = \dfrac{\sigma }{{2{\varepsilon _0}}}$ (1)
Where,
E is the value of electric field,
$\sigma $ is charge density of the plate,
${\varepsilon _0}$ is the permittivity of vacuum.

Potential difference between two plates is given as:
$V = Ed$ (2)
Where,
V is the potential difference between the plates,
E is the electric field between the plates,
d is distance between the plates.

Charge stored in a capacitor is given by:
$Q = CV$ (3)
Where,
Q is total charge stored,
C is the capacitance of the capacitor.

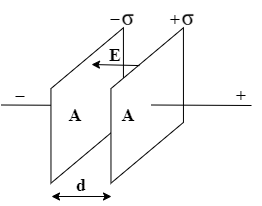
Complete step by step answer:
Assumption: Area of each plate is A. So we get $\sigma = \dfrac{Q}{A}$.

To find: Capacitance C of the parallel plate capacitor.

Step 1
To find the total electric field between the plates first you need to find the field direction for each plate’s field. At any point within the plates direction of electric field due to each plate must be opposite as they are in opposite directions from the point. But here, the charge densities of each plate is different. Hence, using eq.(1) get the total field E within the plates as:
\[E = \dfrac{\sigma }{{2{\varepsilon _0}}} - \dfrac{{( - \sigma )}}{{2{\varepsilon _0}}} = \dfrac{\sigma }{{{\varepsilon _0}}}\] (4)

Step 2
Now, substitute the value of E and $\sigma $from eq.(4) into eq.(2) to get the potential difference as:
$
  V = Ed = \dfrac{{\sigma d}}{{{\varepsilon _0}}} \\
  \therefore V = \dfrac{{\tfrac{Q}{A}d}}{{{\varepsilon _0}}} = \dfrac{{Qd}}{{{\varepsilon _0}A}} \\
 $ (5)

Step 3
Use the value of V obtained in eq.(5) in eq.(3) to get the value of C as:
$
  Q = C \times \dfrac{{Qd}}{{{\varepsilon _0}A}} \\
   \Rightarrow 1 = C \times \dfrac{d}{{{\varepsilon _0}A}} \\
  \therefore C = \dfrac{{{\varepsilon _0}A}}{d} \\
 $

Final answer:
The expression for the capacitance for parallel plate capacitor is $C = \dfrac{{{\varepsilon _0}A}}{d}$.

Note: While doing the derivation we have used the formula for infinite charged sheet but these capacitor plates have finite dimension. Here, the electric field remains uniform straight line perpendicular to the plates but at the edges they take rounded shape and show non-uniform nature. This effect is known as the fringing effect. But practically this doesn’t affect much at the value of the capacitance.