Question

Derive an expression for the bandwidth of interference fringes in Young’s double slit experiment.

Answer 1

Hint: In order to derive this expression first we will understand what Young's double slit experiment is. This experiment states that when a monochromatic light is passed through two narrow slits illuminates a distant screen; a characteristic pattern of bright and dark fringes is observed which is caused by the superposition of overlapping light waves originating from the two slits.

Complete step-by-step answer:

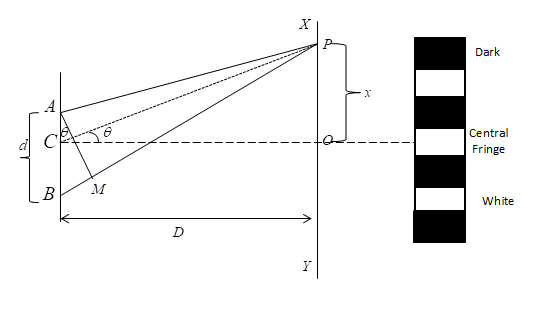
Let d be the distance between the two coherent sources AB. Also XY is the screen placed parallel to the source at a distance D. C is the midpoint of AB
Construction- Draw AM perpendicular to PB.
The path difference S = BP-AP
Therefore AP = MP
Also, BP-AP = BP-MP = BM
For constructive interference path difference must be equal to $n\lambda $
$
  BP - AP = n\lambda \\
  n = 0,1,2,3........ \\
$
From the diagram above
\[B{P^2} - A{P^2} = \left[ {{D^2} + {{\left( {x + \dfrac{d}{2}} \right)}^2}} \right] - \left[ {{D^2} + {{\left( {x - \dfrac{d}{2}} \right)}^2}} \right]\]
Solving the above equation, we get
$
  B{P^2} - A{P^2} = 2xd \\
  \left( {BP - AP} \right)\left( {BP + AP} \right) = 2xd \\
$
Approximately, OC = AP = BP = D
$
  \left( {BP - AP} \right)2D = 2xd \\
  BP - AP = \dfrac{{xd}}{D} = n\lambda \\
$
For n fringes, it is given as
${x_n} = \dfrac{{n\lambda D}}{d}$
Where n = 0, 1 , 2 ,3 ……………. And depending upon the positive value of integers gives bright fringes and negative integers give dark fringes.
 Now, since the fringes are equally spaced the distance between two consecutive bright or consecutive dark fringes gives the fringe width.
$
  \beta = {x_{n + 1}} - {x_n} \\
  \beta = \dfrac{{\left( {n + 1} \right)\lambda D}}{d} - \dfrac{{n\lambda D}}{d} \\
  \beta = \dfrac{{\lambda D}}{d} \\
$
 Where $\beta $ is the bandwidth of the fringe

Note- The above expression for fringes can also be derived without taking the assumptions and the results we get will be the same. The assumption we made here is D should be large, the distance between the two sources is very small. This experiment helps in understanding the waves theory of light.