Question

Derive an expression for electric potential due to a point charge:

Answer 1

Hint: In this question we will use the expression for potential difference and electric field, substituting the values will help us to get the required result. Further, we will study the basics of potential and electric field for our better understanding.

Formula used:
${V_{BA}} = {V_B} - {V_A} = - \int_A^B {E.ds} $
$E.ds = \left[ {k\dfrac{q}{{{r^2}}}} \right]\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}\to
 {r} .ds$

Complete answer:
Let us consider a point charge q, when we move from point A to point B from the charge q, so the change in electric potential is given as:
${V_{BA}} = {V_B} - {V_A} = - \int_A^B {E.ds} $
Now, as we know electric field E is given by the ratio of charge and square of radial distance, so the above equation becomes:
$E.ds = \left[ {k\dfrac{q}{{{r^2}}}} \right]\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}\to
 {r} .ds$
Here, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}\to
 {r} .ds = dr$
As we know, the radial distance represented by r determines the work done or the potential.
Now, putting these values in equation (1), we get:
${V_{BA}} = {V_B} - {V_A} = - \int_A^B {E.ds} = - \int_{{r_A}}^{{r_B}} {\left[ {k\dfrac{q}{{{r^2}}}dr} \right]} $
$ \Rightarrow {V_{BA}} = {V_B} - {V_A} = - kq\left[ {( - 1){r^{ - 1}}} \right]_{{r_A}}^{{r_B}}$
$ \Rightarrow {V_{BA}} = {V_B} - {V_A} = kq\left[ {\dfrac{1}{{{r_B}}} - \dfrac{1}{{{r_A}}}} \right]$
When we calculate electric potential with some reference r, we here consider that reference point as
${r_A} = \infty $
So, our above equation becomes:
$\therefore V = kq\dfrac{1}{r}$
Therefore, we get the required expression for the electric potential for a point charge.

Additional information:
As we know, potential (V) is defined as the amount of work needed to move one unit of electric charge from a reference point to a specific point in an electric field. S.I unit of potential is Volts or joules per coulomb.
Also, the electric field is defined as the electric force per unit charge:
 $E \propto \dfrac{F}{q}$
Here, F is force exerted or experienced by the object and q is the charge on the object. So, if the electric field at a particular point is known and force is known we can get the charge or if the charge is known we can get the force experienced by the point charge.
 Electric field is radially outward from a positive charge and it is radially inward to a negative point charge. S.I unit of electric field is Newton per coulomb.
As we know, the direction of electric field E is taken to be the direction of force it would exert on the positive test charge.
Following is a diagram of charge flowing in a conductor with electric field direction.

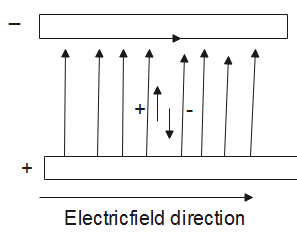
Also, we know that the electric field is defined as the gradient of potential (V):
$E = - gradV$
Since, we know that the surface of the charged conductor has a constant potential. Therefore, there is no field along the surface of the charged conductor. This shows that the electrostatic field at the surface of the charged conductor should be normal to the surface at every point.

Note:
We should remember that when radial distance remains constant then no work is done or we can say no change in the electric potential. Electric field is a vector quantity. It has both magnitude and direction. Electric field inside a conductor is zero, because charges are not present inside the conductor, they are present on the surface of the conductor.