Question

Derive an expression for drift velocity of free electrons in a conductor.

Answer 1

Hint: Consider electrons as infinitesimal free particles in the conductor experiencing force due to an electric field. We can calculate the force on each electron, and find the acceleration. Drift velocity is the average velocity of all the electrons in a given space.

Formula used:
Force on a charged particle in an electric field is given by,
\[F=qE\] ……………… (1)
Where, \[q\] is the charge of the particle, and \[E\] is the electric field.
The general kinematics equation,
\[v=u+at\] …………… (2)
Where,\[v\] is the final velocity,
             \[u\] is the initial velocity,
             \[a\] is the acceleration,
     and \[t\] is the time duration.

Complete step by step answer:
Let’s assume we have an electric field E in the conductor.
For now, we are going to consider only one electron, and calculate the acceleration of the electron due to this electric field.
    

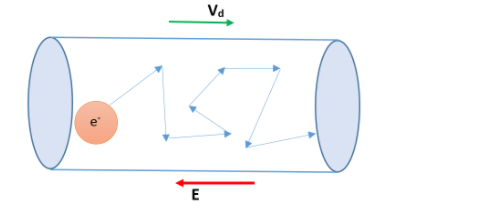
As the force due to the electric field is much more than the electron-electron interaction, we are not going to consider that.
Let’s consider the charge of an electron to be (-e).
Hence, the force on the electron is equal to
\[F=-eE\]
We can find the acceleration of the electron by,
\[a=\dfrac{F}{m}=-\dfrac{eE}{m}\]
Where m is the mass of the electron.
Now, let us introduce a quantity called the relaxation time. It is the average time between two consecutive collisions.
Let’s assume there are ‘n’ number of electrons in the conductor at any given time.
The relaxation time is given by,
\[\tau =\dfrac{{{\tau }_{1}}+{{\tau }_{2}}+{{\tau }_{3}}+{{\tau }_{4}}+....}{n}\]
Where, \[[{{\tau }_{1}},{{\tau }_{2}},{{\tau }_{3}},{{\tau }_{4}},....]\] are the collision times of n electrons.
We can say that the drift velocity is the average velocity of all the electrons.
So, we can write,
\[{{v}_{d}}=\dfrac{{{v}_{1}}+{{v}_{2}}+{{v}_{3}}+{{v}_{4}}+{{v}_{5}}+....}{n}\]
We can use the general kinematics equation,
\[v=u+at\] …………… (2)
Where, \[v\] is the final velocity,
             \[u\] is the initial velocity,
             \[a\] is the acceleration,
     and \[t\] is the time duration.
 Using equation (2) we get,
\[{{v}_{d}}=\dfrac{({{u}_{1}}+{{u}_{2}}+...+{{u}_{n}})+a({{\tau }_{1}}+{{\tau }_{2}}+...+{{\tau }_{n}})}{n}\]
\[\Rightarrow {{v}_{d}}=0+\dfrac{a({{\tau }_{1}}+{{\tau }_{2}}+...+{{\tau }_{n}})}{n}\] -- (Initial average velocity is zero)
\[\begin{align}
  & \Rightarrow {{v}_{d}}=\dfrac{a({{\tau }_{1}}+{{\tau }_{2}}+...+{{\tau }_{n}})}{n} \\
 & \Rightarrow {{v}_{d}}=a\tau \\
 & \Rightarrow {{v}_{d}}=(-\dfrac{eE}{m})\tau \\
\end{align}\]
The expression of drift velocity is,
\[{{v}_{d}}=(-\dfrac{eE}{m})\tau \]

Note:
Students should be clear with the approach. If you know the basic equations, you can easily derive to the above expression. We all know that the vibration of the atoms increases as we heat a conductor. So, the time duration between two collisions decreases. As a result, the relaxation time decreases. The drift velocity is directly proportional to the relaxation time. So, drift velocity will decrease with the increase in temperature.