Question

Derive a formula to measure the rate of flow of a liquid through a Venturimeter.

Answer 1

Hint: To solve these types of questions we must have complete knowledge of a venturimeter. A venturimeter can be defined as a device which can be used to measure the rate of flow of a particular liquid through a pipe. We can say that Bernoulli’s principle is used in a venturimeter for an incomprehensible fluid.

Complete step-by-step solution: -
To derive the formula to measure the rate of flow of a liquid through a venturimeter we must know it’s working and construction. A venturimeter consists of a horizontal tube having two openings, one wide and the other narrow with a cross sectional area of ${{A}_{1}}$ and ${{A}_{2}}$ respectively. Let us assume that the velocity of the fluid at these openings is ${{v}_{1}}$ and ${{v}_{2}}$ at these openings with a pressure of ${{P}_{1}}$ and ${{P}_{2}}$. The diagram of a venturimeter is attached herewith for better understanding:

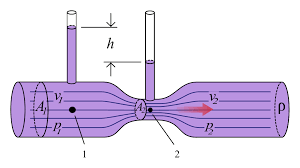
Assuming the flow of fluid to be streamlined with a density of $\rho $ and using Bernoulli’s theorem, we get the equation as:
$\begin{align}
  & {{P}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}={{P}_{2}}+\dfrac{1}{2}\rho v_{2}^{2} \\
 & \Rightarrow {{P}_{1}}-{{P}_{2}}=\dfrac{1}{2}\rho \left( v_{2}^{2}-v_{1}^{2} \right) \\
\end{align}$
Also, we know that the difference in level in the vertical tubes is $h$, thus
${{P}_{1}}-{{P}_{2}}=\rho gh$
On combining both the equations:
$\begin{align}
  & \rho gh=\dfrac{1}{2}\rho \left( v_{2}^{2}-v_{1}^{2} \right) \\
 & \Rightarrow v_{2}^{2}-v_{1}^{2}=2gh-\text{equation }1 \\
\end{align}$
From equation of continuity, we know that:
$\begin{align}
  & {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}} \\
 & \Rightarrow \dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{{{v}_{2}}}{{{v}_{1}}}-\text{equation 2} \\
\end{align}$
From equation $1$, we get:
$v_{1}^{2}\left[ \left( \dfrac{v_{2}^{2}}{v_{1}^{2}} \right)-1 \right]=2gh$
From equation $2$, we get:
$\begin{align}
  & v_{1}^{2}\left[ \left( \dfrac{A_{1}^{2}}{A_{2}^{2}} \right)-1 \right]=2gh \\
 & \Rightarrow v_{1}^{2}=A_{2}^{2}\dfrac{2gh}{A_{1}^{2}-A_{2}^{2}} \\
 & \therefore {{v}_{1}}={{A}_{2}}\sqrt{\dfrac{2gh}{A_{1}^{2}-A_{2}^{2}}} \\
\end{align}$
Hence the rate of flow of a liquid through venturimeter comes out to be:
${{v}_{1}}={{A}_{2}}\sqrt{\dfrac{2gh}{A_{1}^{2}-A_{2}^{2}}}$

Note: The Venturimeter keeps in mind the equation of continuity which means that if a liquid enters a pipe, then it must also leave the pipe from the other end. Hence a venturimeter used Bernoulli’s equation and equation of continuity on a fluid that is incompressible in nature.