Question

Defined the phenomenon of total internal reflection.

Answer 1

Hint: Before we understand the phenomenon of total internal reflection, we have to understand the basic principle of refraction that is important for the understanding of the phenomenon of total internal reflection.
Refraction is defined as the phenomenon in which there is a change in the direction of propagation of a light wave when light enters another medium of different optical density.

Complete answer:
The phenomenon of refraction is governed by the Snell’s law of refraction, which states that–
The ratio of sine of angle of incidence to the sine of angle of refraction is always constant and is equal to the refractive index of the pair of media.
If $i$ is the angle of incidence and $r$ is the angle of refraction of a light wave travelling from a rarer medium 1 to a denser medium 2, as per Snell’s law, we have –
$\dfrac{{\sin i}}{{\sin r}} = {n_{21}}$
where ${n_{21}} = \dfrac{{{n_2}}}{{{n_1}}}$; ${n_2}$ and ${n_1}$ are the absolute refractive indices of the media with respect to air.
Let us consider a case of refraction in which the light wave is travelling from the denser medium 2 to rarer medium 1 as shown:

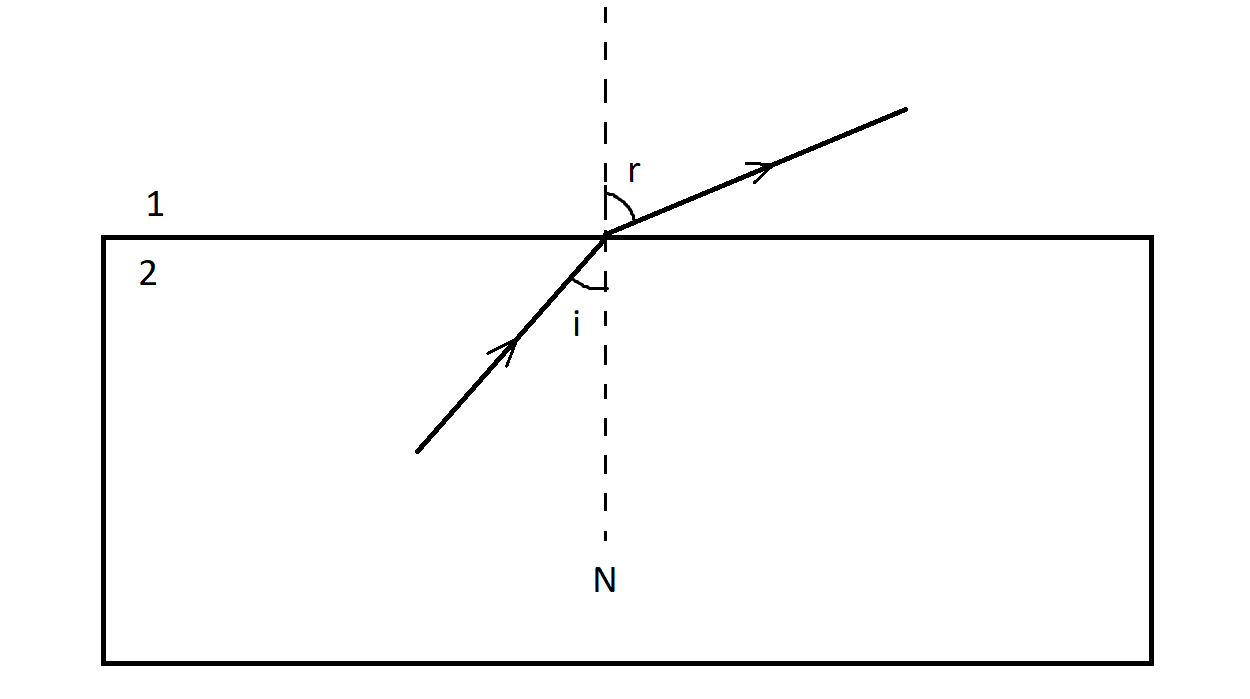
We can see that the refracted light ray is moving away from the normal as shown.
Let us consider a particular angle of incidence known as the critical angle, $i = c$ where the angle of refraction is equal to ${90^ \circ }$ as shown:

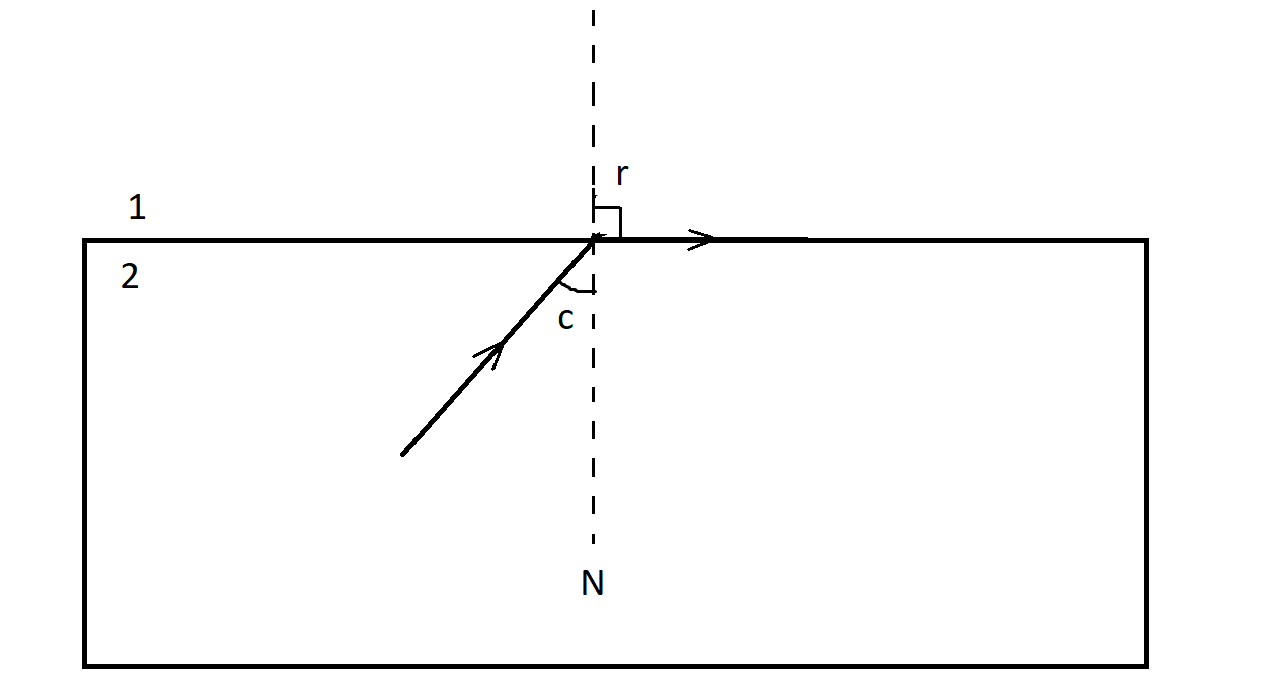At this point, the refracted ray grazes along the surface of the denser medium.
If we increase the angle of incidence beyond the critical angle, $i > c$, we observe that the ray is reflected back inside the medium as shown:

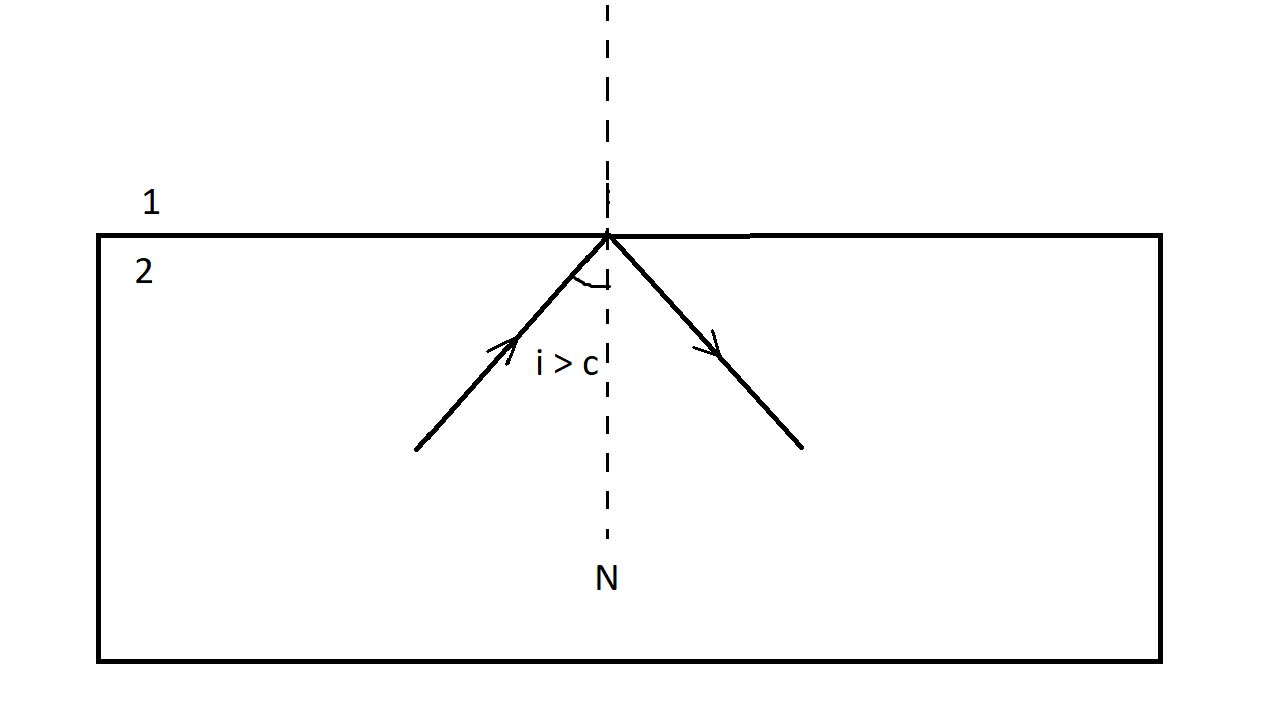This phenomenon wherein the ray undergoes reflection within the medium, instead of refraction, when the incident angle is higher than the critical angle of the denser medium, is called total internal reflection.
We can say that, in order for total internal reflection to occur, the necessary conditions are:
i) Light must travel from denser to rarer medium
ii) Angle of incidence must be greater than the critical angle of the denser medium.
Applications of total internal reflection phenomenon:
i) Artificial indoor lighting using optical fibres.
ii) Fibre communication through the use of optical fibres.

Note: The critical angle of the medium is given by the formula –
$c = {\sin ^{ - 1}}\left( {\dfrac{1}{n}} \right)$
where n = absolute refractive index of the denser medium.
Also, students should note that the concept of critical angle only exists when the light is travelling from denser medium to the rarer medium and not the reverse case.