Question

Define the following term: Intersecting lines.

Answer 1

Hint: In this question, we have been asked to define the term - Intersecting lines. Write the meaning of these lines and explain the concept of point of intersection through a figure. Also tell the difference between other lines and intersecting lines.

Complete step-by-step solution:
We have been asked to define the term ‘intersecting lines’.
Before defining Intersecting lines, we need to know that there are other types of lines as well.
1) Parallel lines – These are a pair of lines which never meet. They do not have an intersecting point and the distance between such lines always remains the same.
2) Overlapping lines – These lines coincide with each other such that only one line can be seen. The equation of these lines is same.
3) Intersecting lines – let us know about intersecting lines in detail.
Intersecting lines –
These are those lines which cut each other at exactly one point in a plane. These lines share a common point which is known as the point of intersection. In this figure, point O is the point of intersection of the lines L and M.

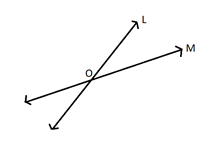
These types of lines have only one meeting (intersecting) point. They do not intersect at more than one point. Also, they can intersect at any angles, more than $0^\circ $ and less than $180^\circ $.

Note: We have to mind that, opposite to the intersecting lines is parallel lines. A parallel lines are lines in a plane which do not meet, two straight lines in a plane that do not intersect at two points are said to be parallel.
Given parallel straight lines l and m in Euclidean space, the following properties are equivalent:
Every point on line m is located at exactly the same (minimum) distance from line l (equidistant lines).
Line m is in the same plane as line l but does not intersect l (recall that lines extend to infinity in either direction).
When lines m and l are both intersected by a third straight line (a transversal) in the same plane, the corresponding angles of intersection with the transversal are congruent.