Question

Define interference of light waves.Draw a diagram of Young’s double slit experiment to produce interference fringe pattern. Derive an expression of fringe width for bright fringes.

Answer 1

Hint: If two light waves from different coherent sources, they disturb each other in terms of energy or intensity. This phenomenon of superposition of two coherent light waves causes formation of dark fringes and bright fringes. The fringe width is the same for dark fringes and bright fringes is the same and depends on the wavelength of the light source, distance between the slits and the distance between the slits and the screen.

Formula Used:
$\Delta x=\dfrac{yd}{D}$
where $\Delta x$ is path difference, y is the vertical position of the fringe, d is the distance between the slits and D is the distance between screen and the slits.
$\Delta x=n\lambda $, formula for nth bright fringe where $\lambda $ is the wavelength.

Complete step by step answer:
The redistribution of the intensity of the light waves due to the superposition of the waves is called interference of light waves.Following is a diagram of Young’s double slit experiment to produce interference fringe pattern.

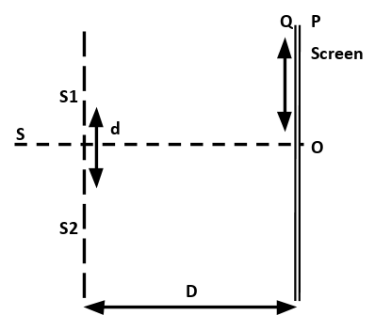
The Young’s double slit experiment consists of a source $S$ placed symmetrically with respect to two slits ${{S}_{1}}$ and ${{S}_{2}}$. A screen is placed in front of the slits. The initial source of light is placed at source $S$ and after that the light wave passes through ${{S}_{1}}$ and ${{S}_{2}}$. Then, a fringe pattern is formed on the screen. The line $SO$ is perpendicular to both the screen and the plane passing through ${{S}_{1}}$ and ${{S}_{2}}$.Distance between the slits is denoted by $d$and that between the slits and the screen is denoted by $D$. The bright fringe formed at $O$ is called the central maximum.

Fringe width is the vertical width on the screen between any two consecutive bright fringes or two consecutive dark fringes.Let us now derive the expression for fringe width for a given Young’s double slit experiment. The path different between the two sources at a point the screen is given as $\Delta x=\dfrac{yd}{D}$
For the points where bright fringes are formed, the path difference is given as,
$\Delta x=n\lambda $
With we get that for nth bright fringe, $\dfrac{yd}{D}=n\lambda $
$\Rightarrow y=n\lambda \dfrac{D}{d}$
For two consecutive bright fringes (i.e. nth and (n+1)th bright fringe) we can write that
${{y}_{1}}=n\lambda \dfrac{D}{d}$
And
${{y}_{1}}=(n+1)\lambda \dfrac{D}{d}$
By definition of fringes width, $\beta ={{y}_{2}}-{{y}_{1}}$.
Therefore,
$\Rightarrow \beta =(n+1)\lambda \dfrac{D}{d}-n\lambda \dfrac{D}{d}$
$\therefore \beta =\lambda \dfrac{D}{d}$

Hence, the fringe width in a given setup of a young's double slit experiment is equal to $\beta =\lambda \dfrac{D}{d}$.

Note:The light sources needed for Young’s double slit experiment to produce interference fringe pattern must be coherent, that is the source of light must be of the same frequency. Also, in the interference, the energy is redistributed in space, but there is no loss of energy.Note that the fringe width is the same for all fringes, either dark fringe or dark fringe. Both the slits should have the same width.You may also derive the expression for fringe width with the help of path difference for dark fringes. You will get the same expression.