
Define an identity function and draw its graph, also find its domain and range.
Answer
506.7k+ views
Hint:We are given a question asking us to define an identity function and then graph it and further, find the function’s domain and range. An identity function is one that has each of its elements in the domain and has an image of itself in the range. The function for the same can be defined as, \[f:R\to R\] we have, \[f(x)=x\] for all values of x belonging to R, \[x\in R\], is the identity function on R. We will graph the function, which will give us a straight line passing through origin. The domain and range can clearly be obtained from the functions definition. Hence, we will have the required function.
Complete step by step answer:
According to the given question, we are asked to define an identity function and draw the graph of the respective function and then we have to mention the function’s domain and range.
An identity function is one that has each of its elements in the domain and has an image of itself as the range.
The function can be defined as,
\[f:R\to R\], \[f(x)=x\] for all values of \[x\in R\]
That is, \[y=x\]
So, we have the function as, \[y=f(x)=x\]
We will draw the graph of this function and for that, we will plot some points and we have,
That is, for any value of ‘x’, the function has same value.
We get the graph as,
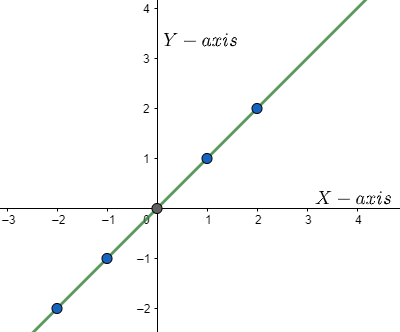
We can see that the graph is a straight line passing through the origin.
And it is defined from the set of real numbers. So, we have the domain and the range as the set of all real numbers, that is,
Domain of the function = R
Range of the function = R
Note: The identity function should be confused with the function having 1 in the range. Also, to graph any function, always find the coordinates first and not do it directly, so as to reduce the risk of getting the graph wrong. The domain refers to the values of the ‘x’ and range refers to the values of \[f(x)\] or ‘y’.
Complete step by step answer:
According to the given question, we are asked to define an identity function and draw the graph of the respective function and then we have to mention the function’s domain and range.
An identity function is one that has each of its elements in the domain and has an image of itself as the range.
The function can be defined as,
\[f:R\to R\], \[f(x)=x\] for all values of \[x\in R\]
That is, \[y=x\]
So, we have the function as, \[y=f(x)=x\]
We will draw the graph of this function and for that, we will plot some points and we have,
| \[x\] | -2 | -1 | 0 | 1 | 2 |
| \[f(x)\] | -2 | -1 | 0 | 1 | 2 |
That is, for any value of ‘x’, the function has same value.
We get the graph as,

We can see that the graph is a straight line passing through the origin.
And it is defined from the set of real numbers. So, we have the domain and the range as the set of all real numbers, that is,
Domain of the function = R
Range of the function = R
Note: The identity function should be confused with the function having 1 in the range. Also, to graph any function, always find the coordinates first and not do it directly, so as to reduce the risk of getting the graph wrong. The domain refers to the values of the ‘x’ and range refers to the values of \[f(x)\] or ‘y’.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Explain sex determination in humans with line diag class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Suicide bags of cells are aEndoplasmic reticulum bLysosome class 12 biology CBSE




