Question

Define an equipotential surface. Draw equipotential surfaces
(i) In the case of a single point charge and
(ii) In a constant electric field in Z-direction
Why are the equipotential surfaces about a single charge not equidistant?
(iii) Can electric fields exist tangentially to an equipotential surface? Give reason.

Answer 1

Hint:The equipotential comprises two words, which are, equi and potential. Here, equi means equal and the potential means ability. After defining the equipotential surface, we will then draw equipotential surfaces in terms of different cases given in the question.

Complete answer:
The equipotential surface is the surface across which the potential will be constant. The potential of any two points on the equipotential surface will be the same and the potential difference across any two points on the equipotential surface will be zero. Equipotential surfaces can be observed as both equal gravity potential and equal electric potential surface.As we know that all the surfaces have equal potential, therefore, the work done on moving any charged body will be zero because the potential difference between the two points will be zero.

Now, we will discuss drawing equipotential surfaces in each case given in the question.
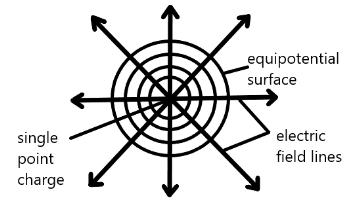
(i) The equipotential surface due to a single point charge will be a concentric sphere having charge at the center.

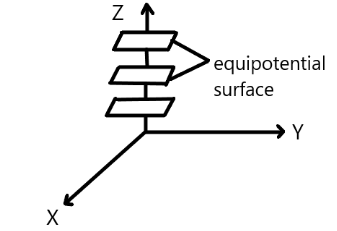
(ii) In a constant electric field along the z-direction, the perpendicular distance between the equipotential surfaces will remain the same.

Now, we know that for a single charge, the equipotential surface will be a series of concentric spheres having charge at center, therefore,
$dr \propto \dfrac{1}{E}$
Here, $dr$ is the separation of the surfaces and $E$ is the electric field.
Therefore, from the above relation, we can say that with the decrease in separation of surfaces, the electric field goes on increasing. That is why, the equipotential surfaces about a single point will not be equidistant.

(iii) The electric field exists tangentially to an equipotential surface because the tangential surface will result in the motion of electrons, but as we have static fields, therefore, the tangential component of the electric field will not exist.

Note:The equipotential surface due to different charges will be different. For a point charge, the equidistant surfaces will be concentric spheres equidistant from the charge. On the other hand, an infinitely long sheet will have equidistant sheets as an equipotential surface. Also, remember that the space between two or more equipotential surfaces having the same potential differences of surfaces will help us to determine the strength of the electric field.