Question

Define absolute refractive index of a medium

Answer 1

Hint: The speed of light depends upon the medium in which it is traveling. And apart from this, there are various other factors that determine the speed of light. Knowing all the factors will help us to define the absolute refractive index.

Complete answer:
Refractive index indicates the speed of light in a given media. The relation is expressed in the form of a ratio, between the speed of light in a vacuum to the speed of light in that given medium.

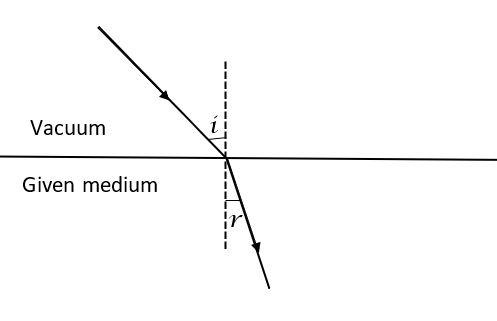
The absolute refractive index is expressed with the help of the symbol n.
The refractive index of a medium depends upon the refractive index of the surrounding. By surrounding we mean the surrounding in which the light ray is passing from into the medium. The Refractive index also depends upon optical density, the wavelength of the light, and temperature.

Additional Information:
The value of the refractive index of light determines the extent to which the light will be refractive when entering or leaving the substance. According to the laws of nature, no substance can travel faster than the speed of light in a vacuum. Those materials with large indices of refraction are known as optically dense media.

Note:
Refractive index is directly proportional to the optical density. It is considered inversely proportional to the wavelength of light.
As the wavelength of light decreases the velocity of the light increases. We know that the absolute refractive index of a medium is equal to the ratio between the speed of light in the air (in this case air signifies vacuum) and the speed of light in that medium. If the velocity of light changes the refractive index of the medium in case of the light of that specific wavelength will also change.