Question

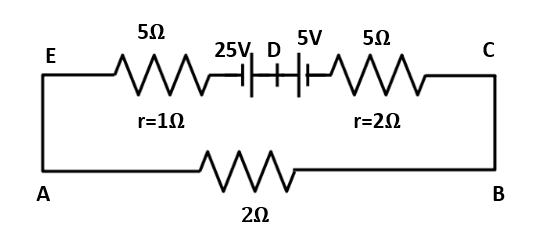
What is the current in the following circuit?

a) $\dfrac{3}{5}$ A from E to C through D.
b) $\dfrac{4}{3}$ A from E to C through D.

Answer 1

Hint: The value of current is the same by any component in a series system. The total resistance of any series circuit is equivalent to the sum of the separate resistances. The supply voltage in a line circuit is equivalent to the sum of the unique voltage falls.

Complete step-by-step answer:
In the given circuit, the two voltages joined with same terminal.
So, net voltage will be:
$V = (25 – 5 )V$
$\implies V = 20 V$
There are three resistances having two resistances with internal resistance.
$r_{1} = 1 \Omega$; $r_{2} = 1 \Omega$
$R_{1} = 5 \Omega$
$R_{2} = 5 \Omega$
$R_{3} = 2 \Omega$
Total resistance is equal to the sum of all resistances.
$ R_{total} = r_{1} + r_{2} + R_{1} + R_{2} + R_{3}$
$\implies R_{total} = 1 + 2 + 5 + 5 + 2$
$\implies R_{total} = 15 \Omega$
We need to calculate the current.
$\text{Current} = \dfrac{\text{voltage}}{\text{resistance}}$
$I = \dfrac{20}{15} A$
$\implies I = \dfrac{4}{3} A$
This current will go from E to B through D.

So, the correct answer is “Option b”.

Note: The value of current in a series line is the same by any component in the system. This is because there is only one way for current flow in a series circuit. Because electric charge passes through conductors, the flow rate at any time in the circuit must be equivalent to the specific point in time.