Question

Cube has 6 flat faces and ………………………..straight edges.
A) 6
B) 8
C) 10
D) 12

Answer 1

Hint:
Here we have to find the number of straight edges in a cube. A cube is a three-dimensional figure and it is bounded by the square on all sides. Here, we will draw the diagram of a cube and count the number of edges and vertices to complete the sentence.

Complete step by step solution:
We know that a face is any flat surface. The flat surface which makes all the sides of the cube is known as the face. So the cube has 6 flat faces. An edge is the line segment where two faces meet. The vertex is a point where two edges meet.
The properties of a cube include that the cube has all its faces in a square shape. Thus six faces are in square shape. All the faces or sides have equal dimensions. The plane angles of the cube are the right angle. Each of the faces meets the other four faces. Each of the vertices meets the three faces and three edges. The edges opposite to each other are parallel.
We will draw a diagram of the cube.

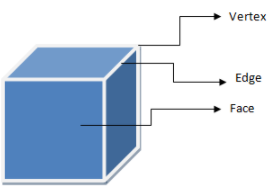
From the figure, we can say that a cube has 6 faces, 8 vertices and 12 edges.
Therefore, the cube has 6 flat faces and 12 straight edges.

Thus Option(D) is correct.

Note:
We can find the number of faces, number of edges, number of vertices for any solid shape using the Euler’s formula. Euler’s formula can be written as the number of faces plus the number of vertices minus the number of edges equals to 2. This can be written as \[F + V - E = 2\]. We know that cube has 6 faces and 8 vertices, we have
\[\begin{array}{l}6 + 8 - E = 2\\ \Rightarrow E = 14 - 2\\ \Rightarrow E = 12\end{array}\]
Thus the number of edges in a cube is 12. This can be solved only if two quantities are known.