Question

How do you convert $r = 4\csc \left(x\right)$ into cartesian form?

Answer 1

Hint: First thing you need to do is to write the equations of the conversion of cartesian to polar that is $x = r\cos \left(\theta \right)$ and $y = r\sin \left(\theta \right)$. Then find the conversion of polar to cartesian. You can convert the 4csc(x) to sin(x). Then you get the final answer for the cartesian coordinates.

Complete step by step solution:
Here is the step wise solution. The first step to do in order to solve this question is to write the above 4csc(x) in terms of sine or cosine. Since cosec is the reciprocal of sine, we write it in terms of sine. Therefore, we get
$\Rightarrow r = 4\csc x = \dfrac{4}{\sin x}$
Now we have to take sinx the left hand side, to get the form of polar coordinates.
The form of polar coordinates is given by, $x = r\cos \left(\theta \right)$ and $y = r\sin \left(\theta \right)$.
Therefore, we get:
$\Rightarrow r = \dfrac{4}{\sin x}$
$\Rightarrow r\sin x = 4$

From here, we can compare it to the general polar coordinate form. We can see that the above equation can be compared to the y polar coordinate, where y is 4. Hence, we get the answer for this as:
$\Rightarrow y = 4$
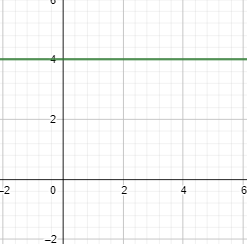
Therefore, we get the final answer for the question, how do you convert $r = 4\csc \left(x\right)$ into cartesian form as $ y = 4$.

Note:You need to know the trigonometric identities to solve this question. You should also know the conversion of cartesian to polar coordinates, which is given in the above hint. Also, note that y = 4 is a horizontal line parallel to the x axis and is at a height of 4 from the x axis.