Question

Construct the following angles and verify by measuring them by a protector: \[105^\circ \]

Answer 1

Hint: Here, we will make the given angle in \[90^\circ \] and then a bisector of \[30^\circ \]. First, we will draw a ray OA and then taking O as center and any radius, draw an arc cutting OA at B. Then with B as center and same radius as before, we will draw an arc intersecting the previously drawn arc at point C and with C as center, same radius, draw another arc intersecting the previously drawn arc at point D. Then we will draw ray OE passing through C and a ray OF passing through D and take C and D as center, with radius more than \[\dfrac{1}{2}CD\], we will draw arcs intersecting at P and join OP. Then taking Q and C as center, with radius more than \[\dfrac{1}{2}QC\], we will draw arcs intersecting at R and join OR to find the required angle.

Complete step-by-step answer:
We are given that the angle is \[105^\circ \].
Rewriting the given angle, we get
\[
   \Rightarrow 105^\circ = 90^\circ + 15^\circ \\
   \Rightarrow 105^\circ = 90^\circ + \dfrac{{30^\circ }}{2} \\
 \]

So to make the given angle, we will make \[90^\circ \] and then a bisector of \[30^\circ \].

First, we will draw a ray OA.

Taking O as center and any radius, draw an arc cutting OA at B, we get

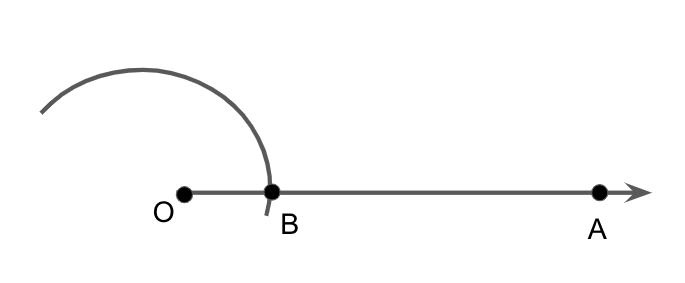
Now with B as center and same radius as before, we will draw an arc intersecting the previously drawn arc at point C and with C as center, same radius, draw another arc intersecting the previously drawn arc at point D, we get

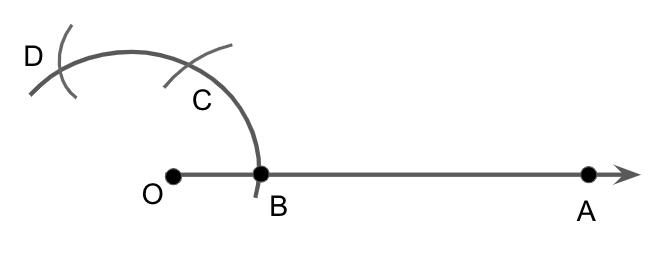
We will now draw ray OE passing through C and a ray OF passing through D, we get

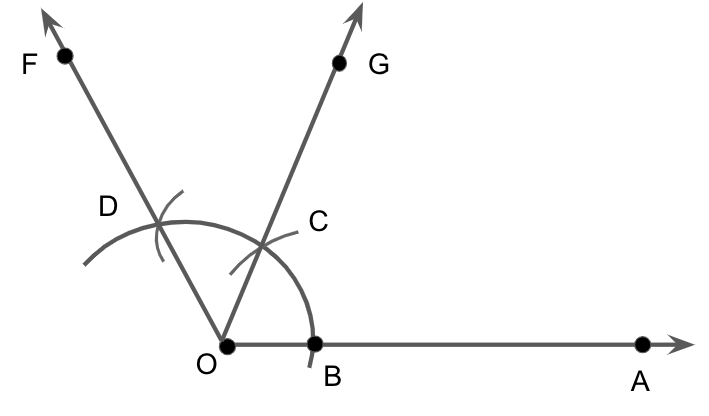
Thus, we have \[\angle AOE = 60^\circ \] and \[\angle EOF = 60^\circ \].

Now we bisect \[\angle EOF\] twice as \[60^\circ \to 30^\circ \to 15^\circ \].

Taking C and D as center, with radius more than \[\dfrac{1}{2}CD\], we will draw arcs intersecting at P and join OP, we get

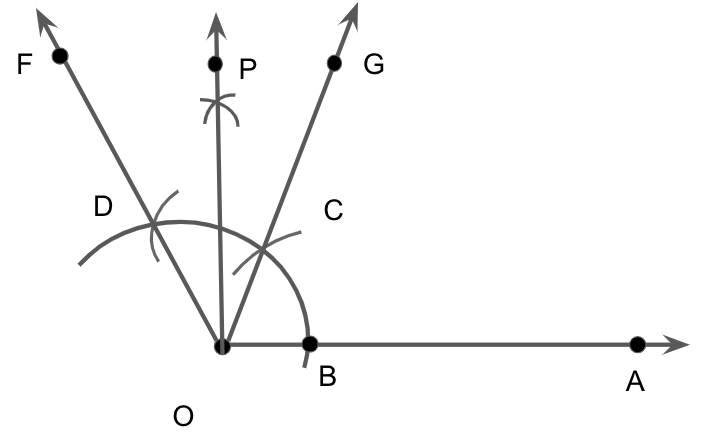
Thus, we have \[\angle AOP = 90^\circ \] and \[\angle POD = 30^\circ \].

Now we bisect \[\angle POD\] twice as \[\dfrac{{30^\circ }}{2} = 15^\circ \] and mark point Q where OP intersects the arc.

Taking Q and C as center, with radius more than \[\dfrac{1}{2}QC\], we will draw arcs intersecting at R and join OR, we get

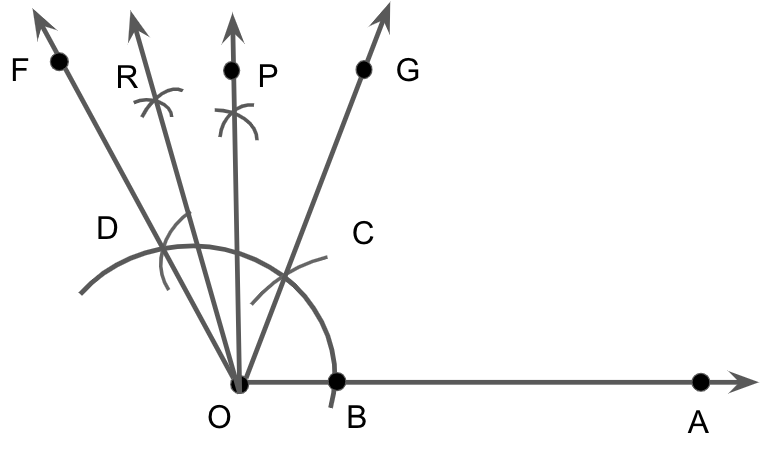
Therefore, \[\angle AOR = 105^\circ \].

On measuring this angle \[\angle AOR\] by protractor, we find that \[\angle AOR = 105^\circ \].
Hence, verified.

Note: The crucial part of this problem is to use the compass properly. One needs to know the basic rules and way of using a compass. We will verify our angle by using the protractor and putting it on the line OA with O as a center. This is a simple problem, we have to be careful with the labeling of the arcs as well.