Question

Construct an isosceles triangle whose base is \[8cm\] and altitude is \[4cm\] and then another triangle whose sides are \[1\dfrac{1}{2}\] times the corresponding sides of the isosceles triangle.

Answer 1

Hint: To draw an isosceles triangle, we will first draw the base (say \[AB\]) whose length is \[8cm\]. Then making the perpendicular bisector of \[AB\], we will get a perpendicular bisecting the line \[AB\] into two equal halves. We are given that the altitude which is the height of the triangle is \[4cm\] so we will put a mark (name it as C) on the perpendicular bisector. So, we have the required isosceles triangle. Now using this triangle as the base we will extend \[1\dfrac{1}{2}\] from side to get another triangle which is \[1\dfrac{1}{2}\] times the isosceles triangle we made first. Isosceles triangle is a triangle which has two sides of same length and one side different.

Complete step-by-step solution:
According to the question we first have to make an isosceles triangle of the given measurement and then make another triangle which is \[1\dfrac{1}{2}\] times greater.
We will proceed in a stepwise manner, so as not to make mistakes.
Step 1: Draw a line (say \[AB\]) of the length \[8cm\], we get

Step 2: Make an angle bisector of the line segment \[AB\], by taking A and B as centres and making an arc both above and below the line segment and joining them, we get

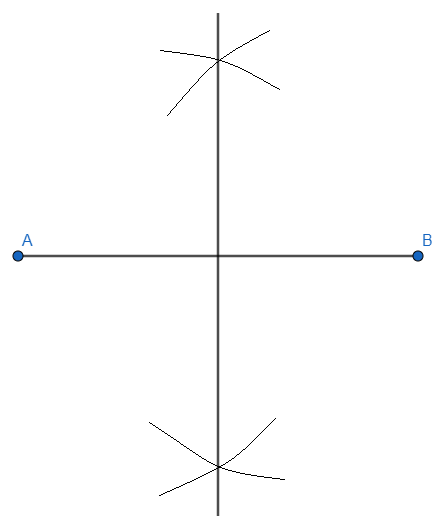
Step 3: We are given that the height of the triangle is \[4cm\], mark an arc on the perpendicular bisector at \[4cm\] from the line segment \[AB\].

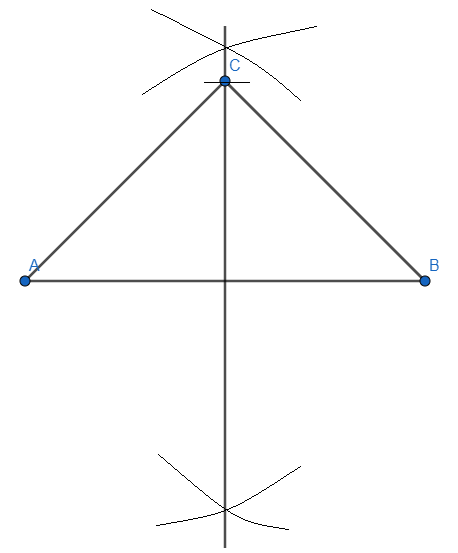
We have the required isosceles triangle and now using this as a base we will draw another triangle which is \[1\dfrac{1}{2}=\dfrac{3}{2}\] times bigger.
Step 4: From point A, we will draw a ray, and since the ratio given is \[\dfrac{3}{2}\], we will make three marks of equal length and mark it A1, A2 and A3, we get

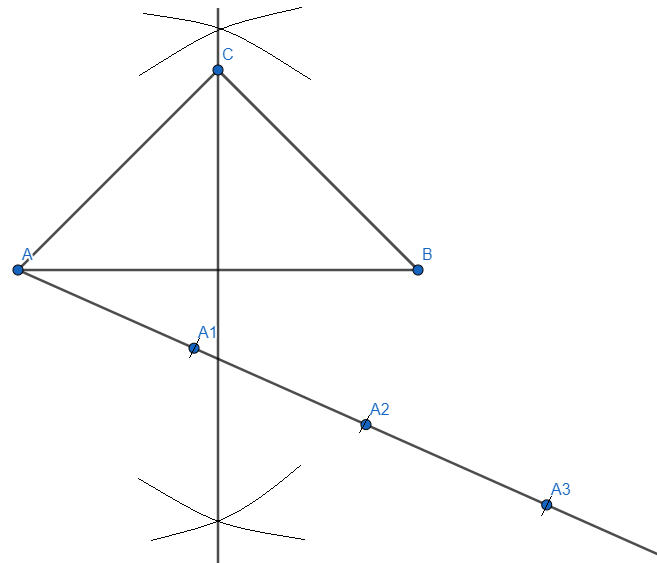
Step 5: We will join A2 to the point B as the ratio given to us is \[\dfrac{3}{2}\]. So, we get,

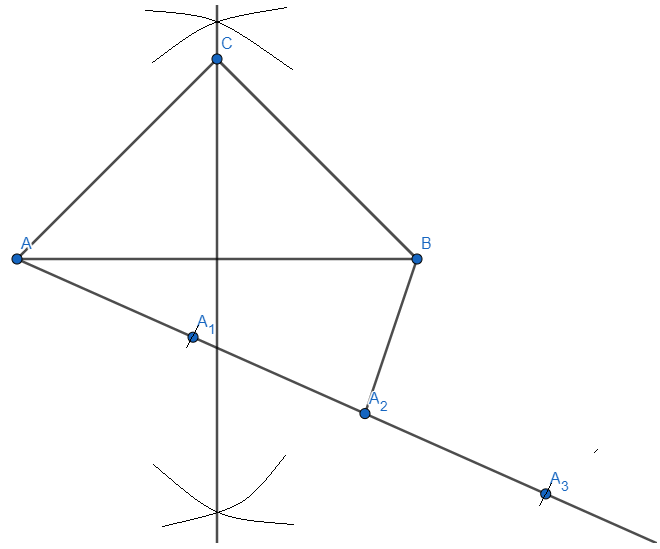
Step 6: We now have to draw line through A3 which is parallel to the line A2B, we will draw the parallel line by measuring the angle between \[\angle B{{A}_{2}}{{A}_{3}}\] and trace it at A3, we get,

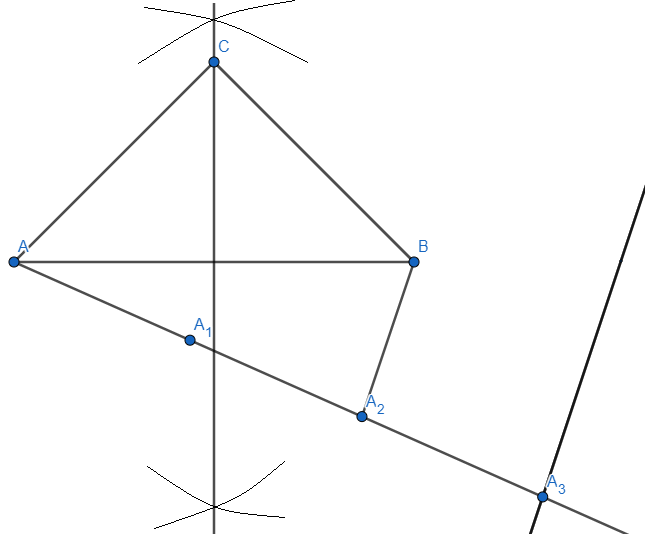
Step 7: Now extending the line segment AB and intersecting the line passing through A3, we get a point (say E)
From E, we draw a line parallel to BC. we get,

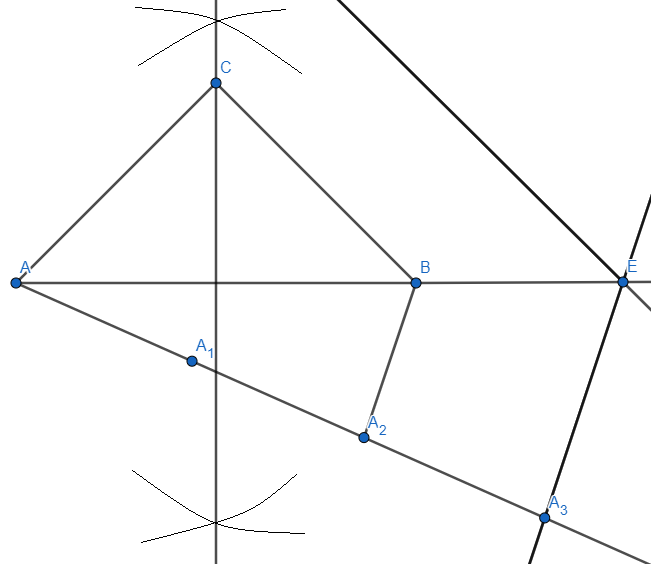
Step 8: we will now extend the line AC so that it intersects to the line extended from the point E and the intersection be named as point F. We get,

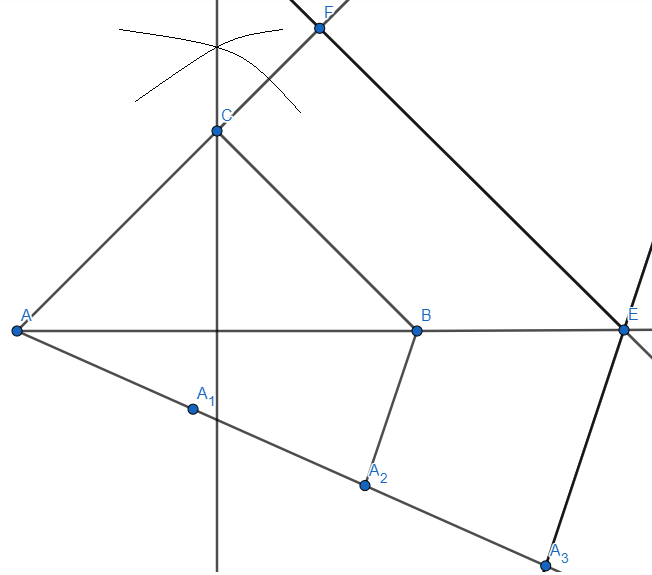
Here, we get the required isosceles triangle AFE which is \[1\dfrac{1}{2}\] times the isosceles triangle ABC.

Note: The measurements should be done neatly to avoid errors. The perpendicular bisector is usually the line that goes through the middle of the line segment so, that can be made accordingly. The parallel lines should be made by measuring the correct corresponding angle, as we know that corresponding angles in parallel are congruent.