Question

Construct a triangle having perimeter $6.4{\text{ cm}}$ and its basic angle are ${60^ \circ }$ and ${45^ \circ }$.

Answer 1

Hint: First, draw a line segment. Then using a protractor draw $\angle XPQ = {60^ \circ }$and $\angle YQP = {45^ \circ }$. Now draw angle bisectors of these angles AP and AQ respectively. Then draw perpendicular bisectors of AP and AQ which intersects the line segment PQ at point B and C respectively. Then join point A and C, and A and B.

Complete step-by-step answer:
We have to construct a triangle with perimeter $6.4{\text{ cm}}$ and with basic angles ${60^ \circ }$ and ${45^ \circ }$.
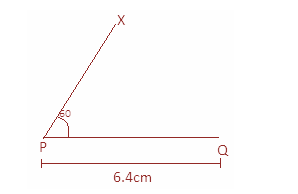
Step 1: Draw a line segment PQ of length $6.4{\text{ cm}}$ using a scale.

Step 2: At point P draw an angle of ${60^ \circ }$ using a protractor so that $\angle XPQ = {60^ \circ }$

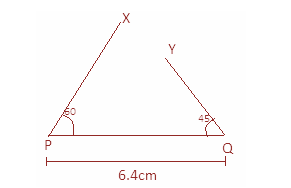
Step 3: Now draw an angle of ${45^ \circ }$ at point Q so that $\angle YQP = {45^ \circ }$

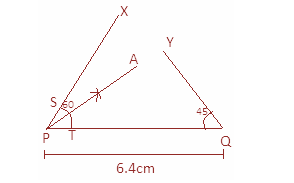
Step 4: Now, we will draw the angle bisector of $\angle XPQ$ by first marking points S and T. Then by taking S and T as centers, draw an arc. Then joint the point of their intersection with point P.

Step 5: Now, we will draw the angle bisector of $\angle YQP$ by first marking points M and N. Then by taking M and N as centers, draw an arc. Then joint the point of their intersection with point Q.

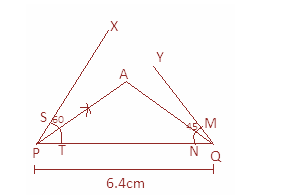
Step 6: Now draw perpendicular bisectors of AP and AQ which intersects the line segment PQ at points B and C respectively.

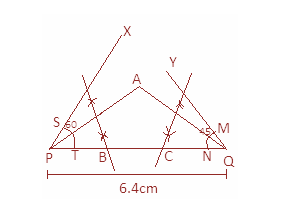
Step 7: Now join AB and Ac to get the required triangle.

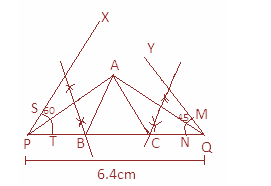
$\vartriangle ABC$ is the required triangle.


Note: Here the student may make mistake if he or she draws the angles facing in the same direction as this-

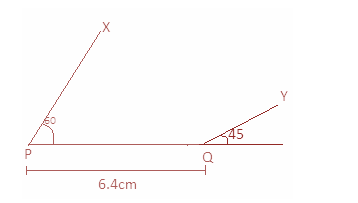
This is wrong because in the first step we have written that PQ is a line segment which means it cannot be extended in any direction. So if we draw the angles like given above then we are contradicting our own statement. Since it is bounded by two distinct points P and Q, hence we make the angle of ${45^ \circ }$ at point Q facing towards the angle drawn at point P.