Question

Construct a regular pentagon in a circle of radius $3.6{\text{cm}}$

Answer 1

Hint: Here, we will first draw a circle with the given radius. Now we will draw the regular pentagon by drawing the central angle of a pentagon with the help of the radii of the circle. We will further construct the regular pentagon by using one side of the pentagon which is drawn using the central angle.

Complete step-by-step answer:
First, we will draw a circle of radius, $r = 3.6{\text{cm}}$
The center of this circle is at point $O$.
Now, we will draw two radii $\overline {OA} $ and $\overline {OB} $ such that $\angle AOB = \dfrac{{360^\circ }}{5} = 72^\circ $
We have divided the angle by 5 because in a pentagon, we have 5 sides and hence, 5 angles.
Now, we will join $AB$
After joining them together, we will consider $A$ as our center and $AB$ as our radius and hence, we will draw an arc which cuts the circle at point $C$. And hence, we will join $AC$.
Now, with $C$ as centre and $AB$ as our radius, we will again draw an arc which cuts the circle at point D and we will join $CD$.
Similarly, we will consider $D$ as our center and draw an arc which finally cuts the circle at point it.
Joining $AB,BC,CD,DE,EB$ will give us the required 5 sides of the regular pentagon.

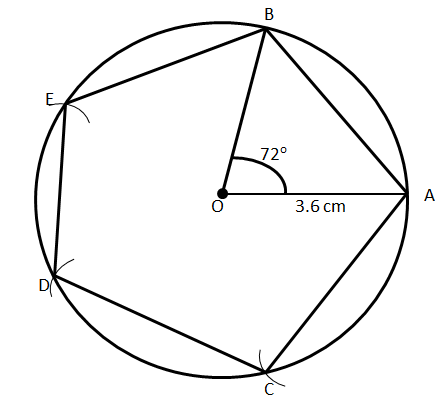
Hence, this is the required regular pentagon inscribed in a circle of radius $3.6{\text{cm}}$
Thus, this is the required answer.

Note: In geometry, a pentagon is a polygon which has five sides. Hence, it is known as a five-sided polygon. In order to calculate the sum of interior angles of any polygon, we use the formula $180^\circ \left( {n - 2} \right)$, where, $n$ represents the number of sides.
Thus, the sum of interior angles of a five-sided polygon is:
$180^\circ \times \left( {5 - 2} \right) = 180^\circ \times 3 = 540^\circ $.
Now, in the case of a regular pentagon, we have all the sides of same length and all the angles of equal measure.
Thus, each angle in a regular pentagon is of $\dfrac{{540^\circ }}{5} = 108^\circ $.
 Also, the central angle of a regular pentagon is of $\dfrac{{360^\circ }}{5} = 72^\circ $