Question

Construct a rectangle \[ABCD\], when its sides are \[6cm\] and \[7.2cm\]. Then, relation between diag. \[AC\] and diag. \[BD\] is
A). \[AC = BD\]
B). \[AC < BD\]
C). \[AC > BC\]
D). Cannot say

Answer 1

Hint: Here we are asked to construct a rectangle \[ABCD\] with the measurements \[6cm\] & \[7.2cm\] and also we have to find the relation between \[AC\] and \[BD\]. First, we will construct the rectangle with the given measurements then by using the properties of the rectangle we will find the relation between \[AC\] and \[BD\].
Formula: The property that we need to know before solving this problem:
If \[ABCD\] be a rectangle then their opposite sides are equal, that is \[AB = CD\] and \[AD = CB\].
Then \[AC\] and \[BD\] will be equal in length which are the diagonal of the rectangle.

Complete step-by-step solution:
Here we aim to find the relation between the diag. \[AC\] and diag. \[BD\] in the rectangle \[ABCD\] with the sides \[6cm\] and \[7.2cm\]. First, let us construct the rectangle with the given measurements.
Construction:
> Let us draw a line segment \[AB\] of measure \[7.2cm\] using a ruler.
> From the point \[A\] and \[B\] draw two perpendicular lines of measure \[6cm\] each with the help of protractor and ruler and mark the endpoints as \[D\] and \[C\] respectively.
> Join the points \[D\] and \[C\] by a line segment using the ruler which will have the measure \[7.2cm\].

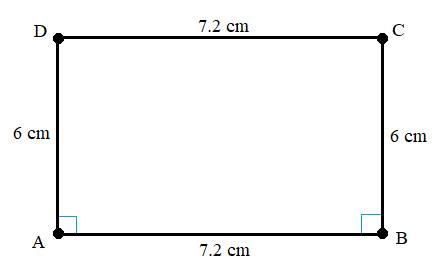
Therefore, we have constructed a rectangle \[ABCD\] with the sides \[6cm\] and \[7.2cm\].
Now we can see that the lines \[AC\] and \[BD\] are the diagonals of the rectangle from the diagram above.

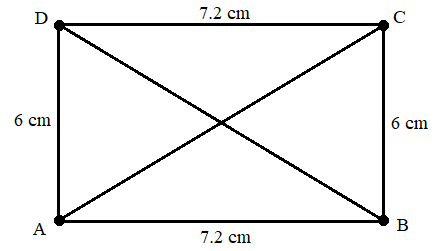
By the property of a rectangle, we know that the diagonals of a rectangle will be the same (equal in measure). Thus, we get that diagonal \[AC\] and diagonal \[BD\] are equal. Now let us find the correct answer from the option.
Option (a) \[AC = BD\] is the correct option as we got the diagonals \[AC\] and \[BD\] are equal.
Option (b) \[AC < BD\] is an incorrect answer as we got \[AC = BD\] from our solution.
Option (c) \[AC > BC\] is an incorrect answer as we got \[AC = BD\] from our solution.
Option (d) Cannot say is an incorrect answer as we got the answer as \[AC = BD\] from our solution.
Hence, option (a) \[AC = BD\] is the correct option.

Note: This problem can also be solved by the following method: After constructing the rectangle draw the diagonals. By drawing the diagonals, we are able to see two right-angle triangles (\[\Delta ABC\] and \[\Delta ABD\]) then by using the Pythagoras theorem we are able to find the measure of two diagonals. After finding their measure by comparing them we can find the relation between them.