Question

Construct a quadrilateral ABCD with AB = 4 cm, BC = 6 cm, CD = 5.6 cm DA = 5 cm and AC = 8 cm. Find also its area.

Answer 1

Hint: To solve this question, we should know the basics of construction of a quadrilateral. Thus, we start with any base (any boundary of the quadrilateral) and then use the constraints in the problem given to construct the quadrilateral.

Complete step-by-step answer:
We first start by noting the given conditions in the question. We have, for required quadrilateral, AB = 4 cm, BC = 6 cm, CD = 5.6 cm, DA = 5 cm and AC = 8 cm. For reference, below is the quadrilateral ABCD with required dimensions as mentioned.
Now, to construct the required quadrilateral, we follow the below steps,
Step 1 - Draw a rough figure and mark the given measurements.
Step 2 - Draw a line segment AB = 4 cm (with the help of a ruler).

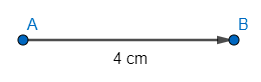
Step 3 - Now, apart from the additional information on the side length, we are also given information about lengths of one of the diagonals. We will make use of this knowledge to perform the next construction. Since, AC = 8 cm and BC = 6cm. With A and B as centres, we draw arcs of radii 8 cm and 6 cm respectively and let them cut at C.

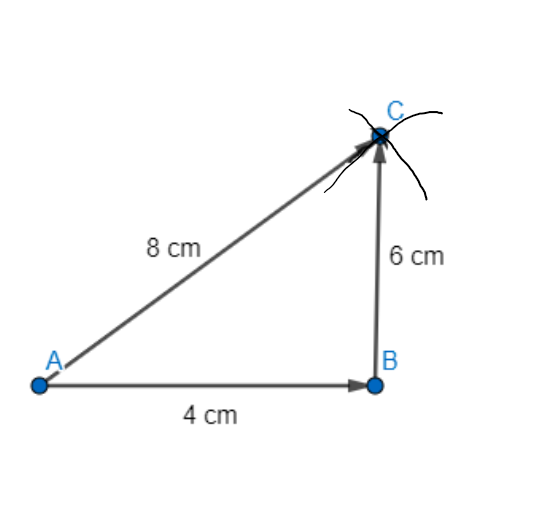
Step 4 - Now, we join BC.
Step 5 - We also know that DA = 5 cm and CD = 5.6 cm. Thus, with A and C as centres draw arcs of radii 5 cm, and 5.6 cm respectively and let them cut at D.
Step 6 - Now, we join AD and CD . Thus, we have ABCD as the required quadrilateral.

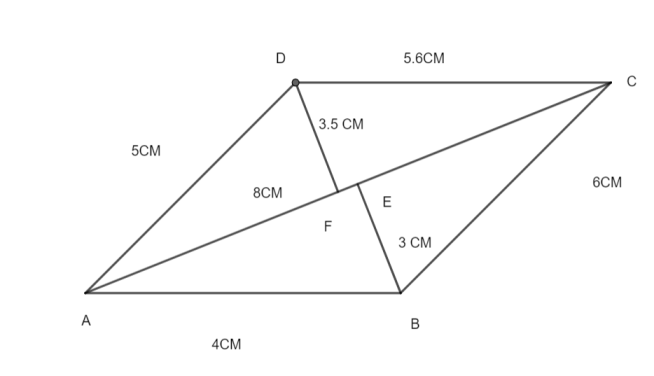
Now, to find the area of this quadrilateral, we make use of the fact that the area of a quadrilateral is the product of half times the length of the diagonal and sum of perpendiculars drawn from the opposite vertices to the diagonal. Thus, from B, we draw BE ⊥ AC and from D, we draw DF ⊥ AC, then measure the lengths of BE and DF. BE = 3 cm and DF = 3.5 cm. Further, the diagonal in this case is AC (which is 8 cm).
Thus, If we have quadrilateral with diagonal a and b and c are length of perpendicular on diagonal, then the area of the quadrilateral is$\dfrac{1}{2}a(b+c)$, where a = diagonal of quadrilateral and b and c are the length of perpendicular on diagonal of quadrilateral.
So, the area of the quadrilateral ABCD will be equals to $\dfrac{1}{2}AC(BE+DF)$
as, AC = 8cm, BE = 3 cm and DF = 3.5cm
= $\dfrac{1}{2}8(3+3.5)$
= 26 $c{{m}^{2}}$

Note: When given a question related to construction, we first start with an information which stands out from the rest of the information. In this case, we were given the extra information about the diagonal, thus we can use this fact to get the first vertex after the base of the quadrilateral. After we get 3 vertices, we can then easily find the fourth vertex easily.