Question

Consider Vernier calipers in which each 1 cm on the main scale is divided into 8 equal divisions and a screw gauge with 100 divisions on its circular scale. In the Vernier calipers, 5 divisions of the Vernier scale coincide with 4 divisions on the mains scale and in the screw gauge, one complete rotation of the circular scale moves it by two divisions on the linear scale. Then:

A. if the pitch of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.01 cm.
B. if the pitch of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.005 mm.
C. if the least count of the linear scale of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.01mm.
D. if the least count of the linear scale of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.005 mm.

Answer 1

Hint: Vernier caliper and screw gauge are two different measuring devices used to make accurate measurements of small readings (less than 1 mm or nearly in that range usually). Least count is the minimum measurable value in an instrument. The Pitch of a screw gauge is the forward movement in the linear scale for one complete rotation of the circular scale. By careful consideration of each option, we can find the answer.

Formula used:
${\text{Least count of screw gauge}} = \dfrac{{{\text{Pitch}}}}{{{\text{Number of divisions in the circular scale}}}}$
Least count of Vernier caliper = 1 Main Scale Division – 1 Vernier Scale Division

Complete step by step answer:
Vernier caliper is a measuring device used to measure readings with a high level of accuracy. Similarly, a screw gauge is also a measuring device used to make accurate measurements of small readings (less than 1 mm or nearly in that range usually). The only major difference between the two measuring devices is that the screw gauge is used only for measuring external measurements, while the vernier caliper is used for both internal as well as external measurements. The visual representation of both these is as follows (the first image is vernier caliper & the second image is screw gauge) :
 

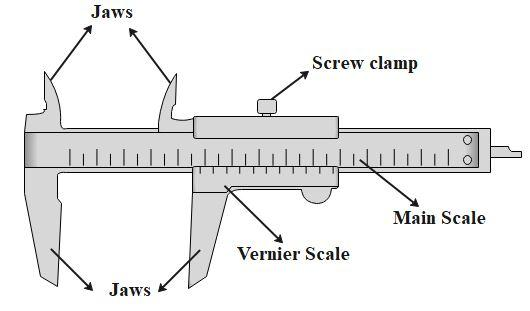
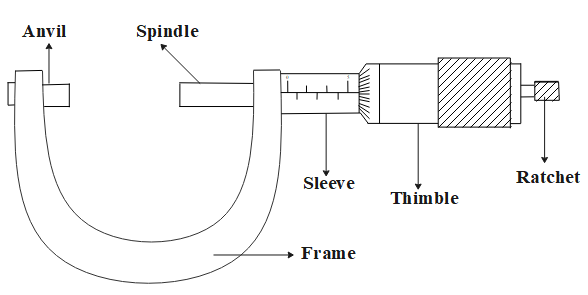
Firstly, let us consider the options A and B, since they seem similar. They state that if the pitch of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.01 cm or 0.005 mm, respectively.
So, firstly let’s calculate the least count of Vernier calipers.
In, Vernier calipers in which each 1 cm on the main scale is divided into 8 equal divisions.
$\eqalign{
  & {\text{8 MSD}} = 1cm \cr
  & \Rightarrow 1{\text{ MSD}} = \dfrac{1}{8}cm \cr} $
Given that 5 divisions of the Vernier scale (VSD) coincide with 4 divisions on the mains scale. So,
$\eqalign{
  & {\text{1 VSD = }}\dfrac{4}{5}{\text{ MSD}} \cr
  & \Rightarrow {\text{1 VSD}} = {\text{ }}\dfrac{4}{5} \times \dfrac{1}{8}{\text{ }}\left[ {\because {\text{MSD = }}\dfrac{{\text{1}}}{{\text{8}}}} \right] \cr
  & \Rightarrow {\text{1 VSD}} = \dfrac{1}{{10}}cm \cr} $
So, least count of Vernier caliper will be given by:
$\eqalign{
  & {\text{LC = 1 MSD - 1VSD }} \cr
  & \Rightarrow {\text{LC}} = {\text{ }}\dfrac{1}{8} - \dfrac{1}{{10}} \cr
  & \therefore {\text{LC}} = \dfrac{1}{{40}}cm \cr} $
So, the pitch of the screw gauge will be given by:
$\eqalign{
  & {\text{Pitch = }}2 \times LCV \cr
  & \Rightarrow {\text{Pitch}} = 2 \times \dfrac{1}{{40}} = \dfrac{1}{{20}} \cr
  & \therefore {\text{Pitch}} = 0.05cm \cr} $
Now, the least count of the screw gauge would be given by after substituting the value of pitch in it, as:
$\eqalign{
  & LC = \dfrac{{{\text{Pitch of the screw gauge}}}}{{{\text{Number of circular scale divisions}}}} \cr
  & \Rightarrow LC = \dfrac{{0.05}}{{100}} = 0.0005cm \cr
  & \therefore LC = 0.005mm \cr} $
So, option B is correct.
Now, when we consider options C and D, we can see that the test condition is if the least count of the linear scale of the screw gauge is twice the least count of the Vernier calipers, the least count of the screw gauge is 0.01mm or 005 mm, respectively.
Now, the pitch of the screw gauge will be given by:
$\eqalign{
  & {\text{Pitch = }}2 \times {\text{Least count of linear scale of screw gauge }} \cr
  & \Rightarrow {\text{Pitch = 2}} \times {\text{2}} \times {\text{LCV}} \cr
  & \Rightarrow {\text{Pitch}} = 4 \times \dfrac{1}{{40}} = 0.1cm \cr} $
Now, the least count of the screw gauge would be given by after substituting the value of pitch in it, as:
$\eqalign{
  & LC{\text{ }} = \dfrac{{{\text{Pitch of the screw gauge}}}}{{{\text{Number of circular scale divisions}}}} \cr
  & \Rightarrow LC{\text{ }} = \dfrac{{0.1}}{{100}} = 0.001cm \cr
  & \therefore LC = 0.01mm \cr} $
So, option C is also correct.
Therefore, in conclusion, the correct options are B and C.

Note:
Least count is defined as the minimum value that can be measured by an instrument. The pitch of a screw gauge is basically the forward distance traveled by the spindle per revolution. This one complete rotation is performed by the circular scale.