Question

Consider three charges, ${q_1} = {q_2} = {q_3} = q$, at the vertices of an equilateral triangle of side $l$. What is the force on a charge Q (with the same sign as q) placed at the centroid of the triangle? Solving using parallelogram law of vectors.

Answer 1

Hint: First we will draw a rough diagram representing all the parameters that are required to us to solve the given problem. Then in that diagram show the line of force that is acting on the center charge. Now using parallelogram theorem to show the resultant force between charge two and four. And from that adding all the force we can get the net force acting on the charge Q.

Formula used:
$F = k\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ along 12.
Where, ${q_1}{\text{ and }}{{\text{q}}_2}$ are the two changes. The distance between the two charges is $r. F$ is the force acting on charge 2 due to 1.

Complete step by step answer:
As per the problem we have three charges, ${q_1} = {q_2} = {q_3} = q$, at the vertices of an equilateral triangle of side l and a change Q which is of same sign as q is placed at the centroid of the triangle.

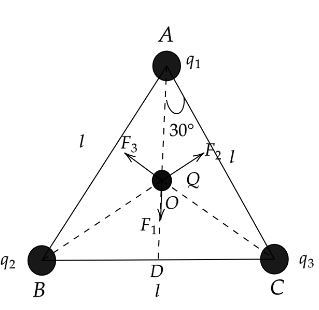
Now as per the figure ABC is an equilateral triangle having side length l, now if we draw a perpendicular line AD to the side BC we will get the angle between line AC and AD is $30^\circ $, as it an equilateral triangle its each angle is equals to $60^\circ $.Hence AD can be written as,
$AD = AC\cos 30^\circ $
We know, $\cos 30^\circ = \dfrac{{\sqrt 3 }}{2}$ and $AC = l$.
Now,
$AD = \dfrac{{\sqrt 3 }}{2}l$
Now in an equilateral triangle the distance of the centroid is to two thirds of the perpendicular line passing through it that is AD.

Now we can write the distance of AO of the centroid o from A as $\dfrac{2}{3}AD$.
Similarly,
$AO = BO = CO = \dfrac{1}{{\sqrt 3 }}l$
Now putting the value of AD from the above calculation we will get,
$\dfrac{2}{3}AD = \dfrac{2}{3}\left( {\dfrac{{\sqrt 3 }}{2}l} \right)$
Cancelling the common terms we will get,
$\dfrac{2}{3}AD = \dfrac{1}{{\sqrt 3 }}l$
Now we can write each of the forces acting on the charge Q as ${F_1}$ be the force on Q due to change q at A.
${F_1} = k\dfrac{{Qq}}{{{{\left( {AO} \right)}^2}}}$ along AO

Now put value of AO we will get,
${F_1} = k\dfrac{{Qq}}{{{{\left( {\dfrac{1}{{\sqrt 3 }}l} \right)}^2}}} \\
\Rightarrow {F_1} = 3k\dfrac{{Qq}}{{{l^2}}}$
${F_2}$ be the force on Q due to change q at B.
${F_2} = k\dfrac{{Qq}}{{{{\left( {BO} \right)}^2}}}$ along BO
Now put value of BO we will get,
${F_2} = k\dfrac{{Qq}}{{{{\left( {\dfrac{1}{{\sqrt 3 }}l} \right)}^2}}} \\
\Rightarrow {F_2} = 3k\dfrac{{Qq}}{{{l^2}}}$
${F_3}$ be the force on Q due to change q at C.
${F_3} = k\dfrac{{Qq}}{{{{\left( {CO} \right)}^2}}}$ along CO

Now put value of CO we will get,
${F_3} = k\dfrac{{Qq}}{{{{\left( {\dfrac{1}{{\sqrt 3 }}l} \right)}^2}}} \\
\Rightarrow {F_3} = 3k\dfrac{{Qq}}{{{l^2}}}$
Now using parallel gram thermo to find the resultant between the two forces ${F_2}{\text{ and }}{F_3}$. As it is an equilateral triangle the two force ${F_2}{\text{ and }}{F_3}$ makes an angle of $120^\circ $. Hence the resultant will be,
$\sqrt {{F_2}^2 + {F_3}^2 + 2{F_2}{F_3}\cos 120^\circ } = \sqrt {{{\left( {3k\dfrac{{Qq}}{{{l^2}}}} \right)}^2} + {{\left( {3k\dfrac{{Qq}}{{{l^2}}}} \right)}^2} + 2\left( {3k\dfrac{{Qq}}{{{l^2}}}} \right)\left( {3k\dfrac{{Qq}}{{{l^2}}}} \right)\left( { - \dfrac{1}{2}} \right)} $

Now on further simplification we will get the resultant of force ${F_2}{\text{ and }}{F_3}$ is $3k\dfrac{{Qq}}{{{l^2}}}$ which along OA.
Now the total force acting on Q will be,
${F_{net}} = {F_{AO}} + {F_{OA}}$
Where, ${F_{AO}}$ is the force along AO and ${F_{OA}}$ is the force along OA.
Now putting the respective values we will get,
${F_{net}} = 3k\dfrac{{Qq}}{{{l^2}}}\widehat r + 3k\dfrac{{Qq}}{{{l^2}}}\left( { - \widehat r} \right)$
$ \therefore {F_{net}} = 3k\dfrac{{Qq}}{{{l^2}}}\left( {\widehat r - \widehat r} \right)$
Where $\widehat r$ is the unit vector along AO.

Therefore the net force acting on the charge Q at the centroid of an equilateral triangle is zero.

Note: We can also solve the problem as fits add all the force acting on the charge Q as ${F_{net}} = {F_1} + {F_2} + {F_3}$. Now,
${F_{net}} = 3k\dfrac{{Qq}}{{{l^2}}}\left( {\widehat {AO} + \widehat {BO} + \widehat {CO}} \right)$
As it is an equilateral triangle the angle between all the sides is $60^\circ $ hence the angle between the unit vectors is $120^\circ $. So they form a triangle of cyclic vectors and the sum of cyclic vectors $\widehat {AO}$,$\widehat {BO}$ and $\widehat {CO}$ is zero. Hence the net force acting on charge Q at centroid of the equilateral triangle is,
${F_{net}} = 3k\dfrac{{Qq}}{{{l^2}}}\left( 0 \right) = 0$