Question

Consider the given plots for a reaction obeying Arrhenius equation \[\left( {{0^ \circ } < T < {{300}^ \circ }C} \right):\] ( ${K_a}$ and ${E_a}$ are rate constant and activation energy, respectively). Choose the correct option.

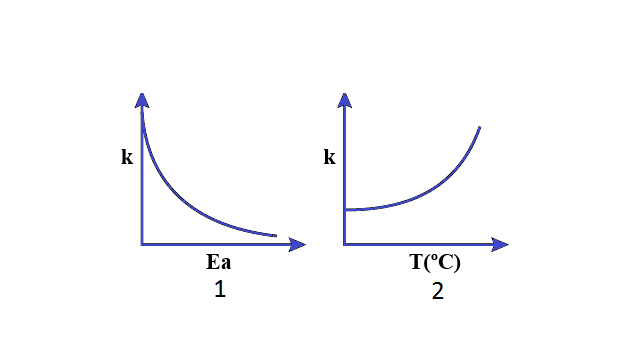
$A.$ Both $1$ and $2$ are wrong
$B.$ $1$ is wrong but $2$ is right
$C.$ Both $1$ and \[2\] are correct
$D.$ $1$ is right but $2$ is wrong

Answer 1

Hint: Before discussing the given plot we should have an idea about the Arrhenius equation ( The Arrhenius equation is a formula for the temperature dependence of reaction rates). This equation was proposed by Svante Arrhenius.


Complete solution:
 The given question can be solved if we find the relation between rate constant, Activation energy and temperature. Now find a relation between these quantities.
Here is the Arrhenius equation,
$k = A{e^{ - {E_a}/RT}}$
Where $A$ is the Arrhenius factor or we can also say frequency factor, $R$ is a gas constant, $T$ is a temperature and ${E_a}$ is the activation energy. Activation energy is measured in joule per mole.
From the above equation it has been found that increasing in temperature or decreasing the activation energy will result in an increase in the rate of the reaction and an exponential increase in rate constant.
Since, we have learned from Arrhenius equation when we increase activation energy $\left( {{E_a}} \right)$ , rate constant $\left( k \right)$ should decrease and if we increase the temperature, power of exponential increase so rate constant $\left( k \right)$ also increase.

Hence the correct option is (C).


Addition information: Activation energy is defined as the minimum amount of extra energy required by a reacting molecule to get converted into a product.


Note: It is to be noted that from the Arrhenius equation we found the rate constant mainly depends on temperature and activation energy. It has found that for a chemical reaction with increase in temperature by ${10^ \circ }$ , the rate constant is doubled.