Question

Consider the following statements.
Statement I The area of the region bounded by lines \[2x+y=4\], \[3x-2y=6\], \[x-3y+5=0\] is \[\dfrac{7}{2}\] sq. units.
Statement II The area of the region \[\left\{ \left( x,y \right):{{y}^{2}}\le 4x,4{{x}^{2}}+4{{y}^{2}}\le 9 \right\}\] is \[\dfrac{9\pi }{8}+\dfrac{1}{3\sqrt{2}}-\dfrac{9}{4}{{\sin }^{-1}}\left( \dfrac{1}{3} \right)\].
Choose the correct option.
A. Statement I is true
B. Statement II is true
C. Both statements are true
D. Both statements are false

Answer 1

Hint: Find the intersection of all the three lines and the three vertices of the triangle. Use the following relation to get area of the triangle
= \[\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|\]
where \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)\] are the vertices of triangle. For the second statement, find the bounded region by relating the inequality of them. Use the relation \[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)\].

Complete step by step answer:
Let us simplify both the statements one by one.
As statement I is given that the area formed by the lines \[2x+y=4\], \[3x-2y=6\], \[x-3y+5=0\] is \[\dfrac{7}{2}\] sq. units.
So let us represent the given equations of lines roughly on the sheet as three lines will intersect at three points and will form a triangle. So, for getting the area bounded by them, we need to find the area of that triangle.
So we get the diagram as,

So let us calculate the intersection point of them and hence apply the identity given as,
Area of triangle = \[\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|.......(1)\]
where, \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)\] are representing the coordinates of three points of any triangle.
So point A can be determined by the lines \[x-3y+5=0\] and \[3x-2y=6\].
Hence we have,
\[3x-2y=6......(2)\]
\[x-3y+5=0.....(3)\]
So let us calculate value of x from equation (3) as,
\[\begin{align}
  & x-3y+5=0 \\
 & x=3y-5.....(4) \\
\end{align}\]
Now put the value of ‘x’ calculated above the equation (2). So we get,
\[\begin{align}
  & 3(3y-5)-2y=6 \\
 & 9y-15-2y=6 \\
 & 7y=21 \\
 & y=\dfrac{21}{7}=3 \\
\end{align}\]
Now put y = 3 to the equation (4). So we get the value of ‘x’ as,
\[x=3(3)-5=9-5=4\].
Hence point A is (4, 3).
Similarly, we can get point B by solving the equation \[2x+y=4\] and \[x-3y+5=0\].
So we have,
\[x-3y+5=0......(5)\]
\[2x+y=4........(4)\]
So value of x from equation (5) as \[x=3y-5......(7)\]
Put \[x=3y-5\] to equation (6). We get,
\[\begin{align}
  & 2(3y-5)+y=4 \\
 & 6y-10+y=4 \\
 & 7y=14 \\
 & y=2 \\
\end{align}\]
Now put the value of y to the equation (7). So we get,
\[\begin{align}
  & x=3(2)-5=6-5=1 \\
 & x=1 \\
\end{align}\]
Hence point B is given as (1, 2).
Similarly, point C can be calculated by the lines \[2x+y=4\] and \[3x-2y=6\].
So we have,
\[2x+y=4.....(8)\]
\[3x-2y=6.....(9)\]
So value of y from the equation (8) can be calculated as,
\[\begin{align}
  & 2x+y=4 \\
 & y=4-2x......(10) \\
\end{align}\]
Put \[y=4-2x\] to the equation (9). So we get,
\[\begin{align}
  & 3x-2(4-2x)=6 \\
 & 2x-8+4x=6 \\
 & 7x=14 \\
 & x=2 \\
\end{align}\]
Put x = 2 in equation (10) as,
\[y=4-2(2)=4-4=0\]
Hence point C is given as (2, 0).
Now we can get the area of \[\Delta ABC\] by the equation (1) as,
Area of \[\Delta ABC\] = \[\dfrac{1}{2}\left| \begin{matrix}
   4 & 3 & 1 \\
   1 & 2 & 1 \\
   2 & 0 & 1 \\
\end{matrix} \right|\]
Now expanding the determinant about Row 1, we get,
Area of \[\Delta ABC\],
\[\begin{align}
  & =\dfrac{1}{2}\left[ 4\left( 2\times 1-0\times 1 \right)-3\left( 1\times 1-2\times 1 \right)+1\left( 1\times 0-2\times 2 \right) \right] \\
 & =\dfrac{1}{2}\left[ 4\times 2-3\left( 1-2 \right)+1(-4) \right] \\
\end{align}\]
\[=\dfrac{1}{2}\left[ 8+3-4 \right]=\dfrac{7}{2}\] sq units.
Area of \[\Delta ABC\] is \[\dfrac{7}{2}\] sq units.
Hence statement I is true.
Statement II: Here we need to determine the area of the region \[{{y}^{2}}\le 4x\] and \[4{{x}^{2}}+4{{y}^{2}}\le 9\] and need to verify whether the area will equal to \[\dfrac{9\pi }{8}+\dfrac{1}{3\sqrt{2}}-\dfrac{9}{4}{{\sin }^{-1}}\left( \dfrac{1}{3} \right)\] or not.
So let us observe the given equations of curves. As we know the standard equation of parabola symmetric about positive x-axis and standard equation of circle with center \[\left( {{x}_{1}},{{y}_{1}} \right)\] and radius ‘r’ are given as,
\[\begin{align}
  & {{y}^{2}}=4ax....(1) \\
 & {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}......(2) \\
\end{align}\]
So if we take the equal sign in the given curves, we get the equation of them as,
\[\begin{align}
  & {{y}^{2}}=4x.....(3) \\
 & 4{{x}^{2}}+4{{y}^{2}}=9......(4) \\
\end{align}\]
As we know \[{{y}^{2}}\le 4x\] region will be either of the side of curve \[{{y}^{2}}=4x\], because we need to include those values of (x, y) which don’t satisfy \[{{y}^{2}}=4x\].
Similarly, \[4{{x}^{2}}+4{{y}^{2}}\le 9\] will be either inside or outside of the circle (as it is a closed shape).
Comparing the equation of circle from (4) to the standard equation of circle i.e. (2). So we can rewrite equation of circle as,
\[\begin{align}
  & 4{{x}^{2}}+4{{y}^{2}}\le 9 \\
 & {{x}^{2}}+{{y}^{2}}=\dfrac{9}{4} \\
 & {{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \dfrac{3}{2} \right)}^{2}}......(5) \\
\end{align}\]
Hence the center of it is (0, 0) and radius is \[\dfrac{3}{2}\].
Now we can represent, \[{{y}^{2}}=4x\] and \[4{{x}^{2}}+4{{y}^{2}}\le 9\] as y-axis.

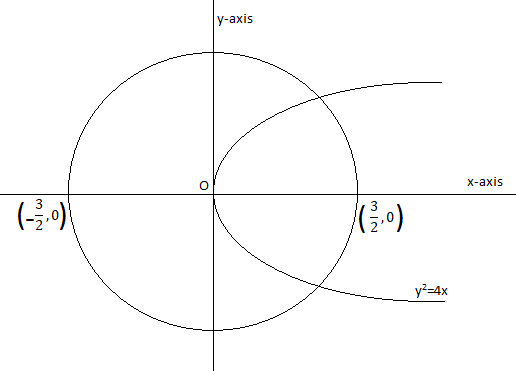
Now we can get the region of \[{{y}^{2}}\le 4x\] by putting values of coordinates to it. As we can write the expression \[{{y}^{2}}\le 4x\] as,
\[{{y}^{2}}-4x\le 0\]
So take (1, 0) to verify the above relation as,
\[\begin{align}
  & {{\left( 0 \right)}^{2}}-4(1)\le 0 \\
 & 0-4\le 0 \\
 & -4\le 0 \\
\end{align}\]
As (1, 0) is satisfying the given relation and (1, 0) is lying inside the curve of the parabola. It means the region by \[{{y}^{2}}\le 4x\] is representing all the points lying inside the curve of \[{{y}^{2}}=4x\] (inside parabola).
Similarly, \[4{{x}^{2}}+4{{y}^{2}}\le 9\] can be verified by putting (0, 0) to it as,
\[\begin{align}
  & 0+0\le 9 \\
 & 0\le 9 \\
\end{align}\]
Hence the region by \[4{{x}^{2}}+4{{y}^{2}}\le 9\] will represent all the points lying inside of the circle. Hence we can represent the individual curves of \[{{y}^{2}}\le 4x\] and \[4{{x}^{2}}+4{{y}^{2}}\le 9\] as,

     

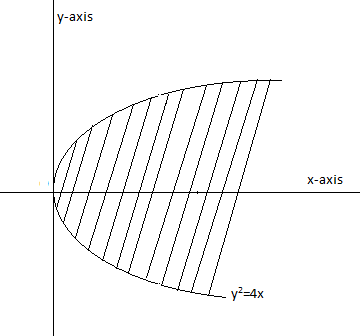
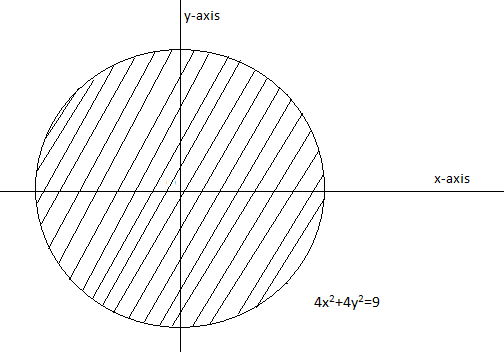
Hence we can represent both the curves together as,

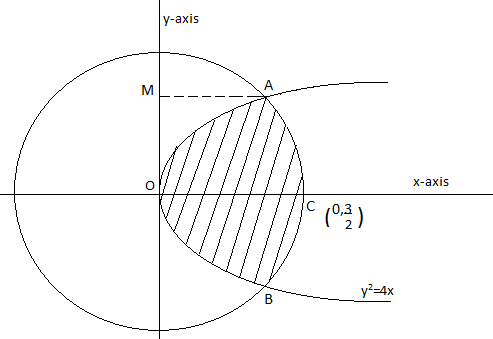
Now we can observe that the area of the shaded region is the same in the first quadrant and fourth quadrant. So total area can be calculated by multiplying the area of the shaded region in the first quadrant by 2.
So the area of the shaded region in the first quadrant i.e. the area of OCAO, can be calculated by the difference of the area of OCAMO and area of OAM.
So let us calculate point A i.e. the point of intersection. So we have,
\[\begin{align}
  & {{y}^{2}}=4x.....(6) \\
 & 4{{x}^{2}}+4{{y}^{2}}=9.....(7) \\
\end{align}\]
Put the value of \[{{y}^{2}}\] as 4x from the equation (6) to the equation (7). So we get,
\[\begin{align}
  & 4{{x}^{2}}+4{{y}^{2}}=9 \\
 & 4{{x}^{2}}+16y=9 \\
 & 4{{x}^{2}}+16x-9=0 \\
\end{align}\]
On factoring, we get,
\[\begin{align}
  & 4{{x}^{2}}+18x-2x-9=0 \\
 & 2x(2x+9)-1(2x+9)=0 \\
 & (2x-1)(2x+9)=0 \\
\end{align}\]
So we get,
\[\begin{align}
  & 2x-1=0 \\
 & x=\dfrac{1}{2} \\
\end{align}\] or \[\begin{align}
  & 2x+9=0 \\
 & x=\dfrac{-9}{2} \\
\end{align}\]
We can ignore \[x=\dfrac{-9}{2}\] as A is lying in the first quadrant, so coordinates of A cannot be negative.
So we get, \[x=\dfrac{1}{2}\]. Put \[x=\dfrac{1}{2}\] to the equation (6) to get the value of y.
\[\begin{align}
  & {{y}^{2}}=4\times \dfrac{1}{2}=2 \\
 & y=\pm \sqrt{2} \\
\end{align}\]
As \[y=-\sqrt{2}\] cannot be the y-coordinate of point A, so ignore \[y=-\sqrt{2}\].
Hence point A is given as \[\left( \dfrac{1}{2},\sqrt{2} \right)\].
So line AM will represent line as \[y=\sqrt{2}\].
So we can get the area of shaded region as,
Area of shaded region = 2 (area of OACO) = 2 [area of OCAM – area of OAM ]…..(8)
Now we can calculate the area of OCAM by integrating the circle w.r.t. ‘y’.
Similarly for area of OAM can be calculated by integrating parabola w.r.t. y, both from y = 0 to \[y=\sqrt{2}\].
So we get values of ‘x’ for circle as,
\[\begin{align}
  & 4{{x}^{2}}+4{{y}^{2}}=9 \\
 & 4{{x}^{2}}=9-4{{y}^{2}} \\
 & {{x}^{2}}=\dfrac{9-4{{y}^{2}}}{4} \\
 & x=\sqrt{\dfrac{9-4{{y}^{2}}}{4}}=\sqrt{\dfrac{9}{4}-{{y}^{2}}}......(9) \\
\end{align}\]
And value of ‘x’ from parabola is,
\[\begin{align}
  & {{y}^{2}}=4x \\
 & x=\dfrac{{{y}^{2}}}{4}.......(10) \\
\end{align}\]
Hence we can get area of shaded region from equation (8) as,
Area of shaded region,
\[\begin{align}
  & =2\left[ \int\limits_{0}^{\sqrt{2}}{\sqrt{\dfrac{9}{4}-{{y}^{2}}}-\int\limits_{0}^{\sqrt{2}}{\dfrac{{{y}^{2}}}{4}}dy} \right] \\
 & =2\left[ \int\limits_{0}^{\sqrt{2}}{\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-{{y}^{2}}}-\int\limits_{0}^{\sqrt{2}}{\dfrac{{{y}^{2}}}{4}dy}} \right] \\
\end{align}\]
We know,
\[\begin{align}
  & \sqrt{{{a}^{2}}-{{x}^{2}}}=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right) \\
 & \int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}} \\
\end{align}\]
So we get,
Area of shaded region,
\[\begin{align}
  & =2\left[ \left( \dfrac{y}{2}\sqrt{{{\left( \dfrac{3}{2} \right)}^{2}}-{{y}^{2}}}+\dfrac{{{\left( \dfrac{3}{2} \right)}^{2}}}{2}\times {{\sin }^{-1}}\left( \dfrac{y}{\left( \dfrac{3}{2} \right)} \right) \right)_{0}^{\sqrt{2}}-\dfrac{1}{4}\left( \dfrac{{{y}^{3}}}{3} \right)_{0}^{\sqrt{2}} \right] \\
 & \\
\end{align}\]
\[=2\left[ \left( \dfrac{\sqrt{2}}{2}\sqrt{\dfrac{9}{4}-2}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2}{3}\sqrt{2} \right)-\left( 0+\dfrac{9}{8}{{\sin }^{-1}}0 \right) \right) \right]-\dfrac{1}{4}\left( \dfrac{{{\left( \sqrt{2} \right)}^{3}}}{3}-0 \right)\]
\[\begin{align}
  & =2\left[ \dfrac{1}{\sqrt{2}}\times \dfrac{1}{2}+\dfrac{9}{8}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{3}-\dfrac{2\sqrt{2}}{12} \right] \\
 & =\dfrac{1}{\sqrt{2}}+\dfrac{9}{8}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right)\times \dfrac{1}{2}-\dfrac{2\sqrt{2}}{12}\times \dfrac{1}{2} \\
 & =\dfrac{1}{\sqrt{2}}+\dfrac{9}{16}{{\sin }^{-1}}\left( \dfrac{2\sqrt{2}}{3} \right)-\dfrac{\sqrt{2}}{12} \\
 & =\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{12}+\dfrac{9}{16}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{3} \\
\end{align}\]
Area of shaded region \[=\dfrac{5\sqrt{2}}{12}+\dfrac{9}{16}{{\sin }^{-1}}\dfrac{2\sqrt{2}}{3}\]
Hence, statement II is false as the area given in the statement is not matching with the actual area.

So option A is the correct answer.
Note:
One may represent the given lines in the statement I axis and can use integration for finding the area bounded by them. But it will be a much longer process than provided in the solution. Don’t calculate the lengths of the sides for calculating area by Heron’s formula, because it will be a much longer process. So be clear with all the approaches for finding the area of the triangle.
Bounded area in the second statement II can also be calculated w.r.t. ’dx’ as well. Areas formed by parabola and circle with the x-axis will be added to each other. It can be given as,

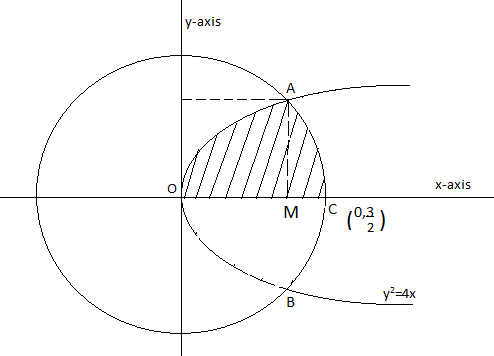
Area of the shaded region in the above diagram would be the sum of the area of OAM and MAC. Calculation is the most important side of this question. So, be careful with the mathematical calculation part.