Question

Consider the following statements in respect of the given equation: ${{\left( {{x}^{2}}+2 \right)}^{2}}+8{{x}^{2}}=6x\left( {{x}^{2}}+2 \right)$.
1.) All the roots of the equation are complex.
2.) The sum of all the roots of the equation is 6.
Which of the above statements is/are correct?
     a). 1 only
     b). 2 only
     c). Both 1 and 2
     d). Neither 1 nor 2

Answer 1

Hint: We will first evaluate the given equation and then in second step we will try to find out sum of roots of obtained equation \[sum\text{ }of\text{ }roots=\dfrac{-b}{a}\]. Then, in the third step we will find the nature of roots of the equation and based on our answer we will choose the correct option.

Complete step-by-step solution-
We have given equation is ${{\left( {{x}^{2}}+2 \right)}^{2}}+8{{x}^{2}}=6x\left( {{x}^{2}}+2 \right)$ and given statements are –
All the roots of the equation are complex.
The sum of all the roots of the equation is 6.
First we will evaluate the given equation as ${{\left( {{x}^{2}}+2 \right)}^{2}}+8{{x}^{2}}=6x\left( {{x}^{2}}+2 \right)$, we know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ we get, ${{x}^{4}}+4+4{{x}^{2}}+8{{x}^{2}}=6{{x}^{3}}+12x$, transposing $6{{x}^{3}},12x$ to left side, we get \[{{x}^{4}}-6{{x}^{3}}+12{{x}^{2}}-12x+4=0\]. We know that the sum of roots of any polynomial equation = $\dfrac{-b}{a}$. We have $b=-6,a=1$ thus sum of roots = $\dfrac{-\left( -6 \right)}{1}=6$. Therefore statement 2 the sum of all the roots of the equation is the correct statement.
We know that \[{{x}^{4}}-6{{x}^{3}}+12{{x}^{2}}-12x+4=0\] is a polynomial function and polynomial function are continuous and differentiable, we will check the value of function $x=0$ and $x=1$ as $f\left( 0 \right)={{\left( 0 \right)}^{4}}-6{{\left( 0 \right)}^{3}}+12{{\left( 0 \right)}^{2}}-12\left( 0 \right)+4=4$and $f\left( 1 \right)={{\left( 1 \right)}^{4}}-6{{\left( 1 \right)}^{3}}+12{{\left( 1 \right)}^{2}}-12\left( 1 \right)+4=-1$. Now, if we represent \[f\left( 0 \right)\text{ }and\text{ }f\left( 1 \right)\] on graph, we get

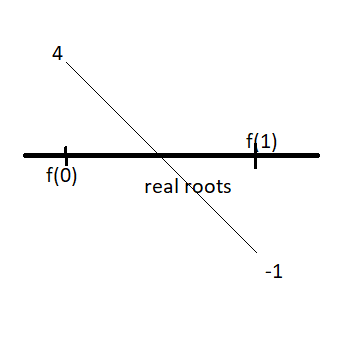
As we can clearly see in the graph that \[f\left( 0 \right)\text{ }and\text{ }f\left( 1 \right)\] is continuous and its interest at x-axis thus at least one real root is possible for the given function. Thus, statement 1 All the roots of the equation are complex is wrong. Therefore only statement 2 is correct and option b) is the correct answer.

Note: For solving the second part we find the values of a given polynomial at any two points and if the values have opposite signs that’s mean function will have the 0 value somewhere between these two points . If at any point the polynomial is 0 then that point would be the root of the given polynomial.